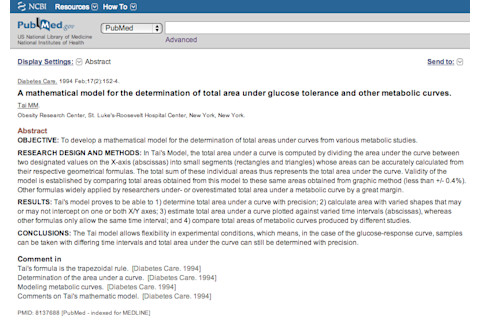
图片:flickr/kawaiikiri这可能对任何人都是一个很好的教训 - 如果你是一名医生,而不是数学家(该死吉姆!),并且你认为你发明了一种新的数学模型来计算曲线下的面积等基本的东西,你应该在发表之前让数学家看看。她会告诉你,是的,你使用许多小矩形的面积来近似曲线下总面积的想法非常好。事实上,它被称为梯形法则,它是牛顿-科茨公式的一部分。就像艾萨克·牛顿一样。但不错的尝试!用于确定葡萄糖耐量和其他代谢曲线下总面积的数学模型。 “目的:开发一种数学模型,用于确定各种代谢研究中曲线下的总面积。研究设计和方法:在Tai模型中,曲线下的总面积通过将X轴(横坐标)上两个指定值之间的曲线下面积划分为小段(矩形和三角形)来计算,这些小段的面积可以从其各自的几何公式中准确计算。因此,这些单独区域的总和代表曲线下的总面积。通过将该模型获得的的总面积与图形方法获得的总面积进行比较(小于+/- 0.4%),可以确定该模型的有效性。研究人员广泛使用的其他公式高估或低估了代谢曲线下的总面积。结果:Tai模型证明能够 1) 精确地确定曲线下的总面积; 2) 计算各种形状的面积,这些形状可能会也可能不会截取在一个或两个 X/Y 轴上; 3) 估计针对不同时间间隔(横坐标)绘制的曲线下的总面积,而其他公式仅允许相同的时间间隔; 4) 比较不同研究产生的代谢曲线的总面积。结论:Tai模型允许实验条件的灵活性,这意味着,在葡萄糖反应曲线的情况下,可以在不同的时间间隔采集样本,并且仍然可以精确地确定曲线下的总面积。”
相关内容:NCBI ROFL:如果你认为你不差劲,你可能确实差劲