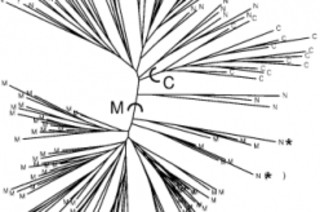
在有 Structure 之前,只有 结构。我的意思是,人口亚结构一直都存在。问题在于我们人类将如何以一种能传达智慧和启迪的方式来表征和可视化它。评估人口亚结构的一种简单方法是,在二维图上可视化个体或种群之间的遗传距离。另一种非常流行的方法是,像左侧那样,在邻接树上表示距离。如您所见,这并不总是令人满意:带有太多尖端的密集树通常几乎不可能解释出最微不足道的推断之外的东西(尽管它们羽毛状的拓扑结构具有美学之美!)。而当邻接树和 MDS 图等图形表示形式删除太多相关信息时,混乱的 Fst 矩阵则有相反的问题。所有距离数据都以其光彩夺目的具体细节存在,但很少有整体理解。
正是在这个混乱的世界中,Structure 柱状图应运而生。当我在 2013 年说“Structure 柱状图”时,我实际上指的是众多基于模型的聚类系统发育软件包。因为速度更快,我更喜欢 Admixture。但 Admixture 实际上只是对 Structure 设定的基本规则的改变。您在右侧看到的是过去五年多来定期出现在本博客上的精美柱状图之一。我已经不厌其烦地重复了它们的作用和不代表的意义,尽管重复一下也无妨。您看到的是 K = 6 时,来自不同人类群体的个体是如何分布的。更详细地说,假设您的个体池可以被认为是六个祖先群体的不同比例的混合。每条线代表一个个体,每条线的比例阴影和特定颜色代表一个特定的 K(对于 K = 6,即群体 1、2、3、4、5、6)。
这时我应该提醒您,这并不意味着这些个体实际上是六个祖先群体的组合。当您仔细思考时,这是常识。仅仅因为有人生成了具有给定 K 的柱状图,并不意味着该柱状图有任何意义。例如,我可以将 K 设置为 666。结果将完全没有价值(甚至邪恶!),但它们将是结果,因为如果您输入垃圾,算法就会产生一些东西(垃圾)。这就是为什么我说人口结构是具体的而且不可言喻的。我们知道它是真实历史的结果,我们可以直观地理解。但是,我们如何为我们的视觉享受和定量精确度生成该结构的地图,则要棘手和滑稽得多。
要真正理解正在发生的事情,回顾介绍 Structure 的原始论文 使用多位点基因型数据推断人口结构 可能会很有用。尽管有后续研究,但该软件包的核心内容都在这份最初的出版物中阐述。基本上,您有一些数据,多位点基因型。由于 Structure 于 2000 年首次亮相,这发生在数十万位点 SNP 芯片数据时代之前。今天,多位点一词听起来几乎有点过时。2000 年,经典的常染色体时代正在衰落,但人们仍然使用 RFLP 等技术。Structure 框架的鲁棒性体现在它平稳地过渡到大规模数据集时代。大致来说,Structure 的三个主要组成部分是经验基因型数据、关于种群动态的正式假设以及强大的计算技术来在前两个要素之间进行映射。用论文的语言来说,您有 X,即个体的基因型,Z,即种群,以及 P,即种群的等位基因频率。它们是多维向量。这里不那么重要的是您只有 X 这一事实。Structure 的真正繁重工作是生成一个向量 Q,它定义了每个个体对祖先种群集合的贡献。这是通过 MCMC 完成的,它在给定数据和内置于软件包中的先验的情况下探索概率空间。尽管有些人似乎将 MCMC 的细节视为一个黑匣子,但实际上对它的工作原理有一些直观的理解通常很有用,尤其是当您想更改默认设置时(确实有些人运行 Structure,但他们不清楚烧入期到底是什么)。最终发生的是,在结构化种群中,基因型不处于 哈迪-温伯格平衡。Structure 正在尝试找到一个能导致种群处于 HWE 的解决方案。
这就引出了我们如何理解结果以及选择哪个 K 值的问题。如果您运行 Structure,您可能会遍历许多 K 值,并重复多次迭代。您可能需要合并重复运行的输出,因为它们会使用不同的算法而有所不同。但无论如何,每次迭代都会生成一个似然值(它源自给定 K 值的数据的概率)。“选择”合适 K 值的最直观方法是简单地等待直到似然值开始趋于平稳。这意味着算法无法在增加 K 值时挤出更多有用的信息。* 这可能看起来枯燥乏味,但它恰恰说明了为什么您不应该从深层次上将任何给定的 K 视为自然的或真实的。K 的选择与现实无关,而更多地与工具性有关。例如,如果您的目标是在全球人口池中检测非洲血统,那么即使更高的 K 值能提供更好的模型拟合(更高的 K 值通常在 MCMC 中需要更长的时间),一个较低的 K 值也足够了。相反,如果您想区分更精细的人口簇,那么无论需要多长时间,谨慎的做法是选择信息量最大的 K 值。
如今,像 Structure、frappe 和 Admixture 这样的基于模型的聚类方法已经成为群体遗传学工具箱中的背景工具。现在有了一些新的方法。TreeMix 这样的软件包利用等位基因频率将过时的系统发育图转换为更具信息量的一组图。其他框架不依赖于逐个位点的独立信息,而是整合位点间的模式,在个体基因组内生成祖先谱系。尽管可以从 Structure 中推断出一些历史信息,但这通常是一个临时的过程,类似于读茶叶渣。连锁不平衡方法具有优势,因为它们明确地探索基因组中的历史过程。但尽管如此,21 世纪初的 Structure 柱状图革命带来了巨大的变革,曾经令人惊叹的东西现在变得司空见惯了。
* 特设的 Delta K 统计量也非常流行。它结合了似然变化率和重复运行之间的变异。