认识到高中数学的很多内容,对我们许多人来说曾是如此令人头疼,而早在几千年前就已被人们深刻理解,这着实令人谦卑。埃及人远未达到“质能方程”E=mc2的水平,但他们知道如何计算金字塔的体积。希腊人没有发明微积分,但他们确实计算出了圆的面积并证明了这一点。从历史的角度来看,这些计算的成就与爱因斯坦或牛顿的成就相比,毫不逊色。
现代世界,拥有数字计算机和内燃机,建立在数字爱好者探索的基础上。对我们来说幸运的是,他们在这方面已经进行了很长时间的研究。
已故的新罕布什尔大学教授大卫·伯顿(David Burton)在他的著作《数学史》中写道:“除天文学外,数学是最古老、持续时间最长的精确科学之一。”
以下是古代一些最伟大的数学成就,摘自该主题最早的一些著作。
1. 截顶金字塔体积
如今,数学的惊人成果在我们周围无处不在,体现在每一座摩天大楼和每一座悬索桥中。然而,很少有东西能像吉萨金字塔那样激发人们的惊叹。它建于大约4600年前,其计算能力在古代世界中是无与伦比的。
恰巧,计算整个金字塔的体积是一件易事:用底面积的三分之一乘以高。通过金字塔和棱柱的微型模型,两者的底面积和高都相同,可以轻松计算出来。用水填充金字塔,然后倒入棱柱中,你会发现棱柱可以容纳整整三倍的体积。由于棱柱的体积就是底面积乘以高,你可以用它来推断金字塔的体积。
一个截顶金字塔(顶部被削掉的金字塔,也称为台体)的体积公式,其复杂程度要高出一个数量级。看
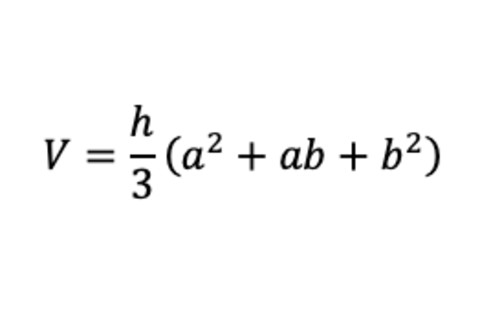
截顶金字塔公式
当然,埃及人并没有那样写,但《莫斯科纸草》(一份大约公元前1850年的数学问题集)表明他们掌握了其中的基本原理。
这比那个时代早得多,伯顿称之为“古代几何学的杰作”。从实际角度来看,这使得他们在建造过程中,能够计算出还需要多少材料来完成工作。
阅读更多: 我们都遇到过的拼图问题的数学解决方案已找到
2. 勾股定理
如果你还记得几何学中的任何东西,那很可能就是这个:在直角三角形中,斜边(最长边)的平方等于其他两条边平方之和。
你可以通过实际绘制从每条边突出的正方形来验证这一点。你也可以将其表示为一个优雅的公式,它可能和你记忆中的“线粒体是细胞的能量工厂”一样深刻。
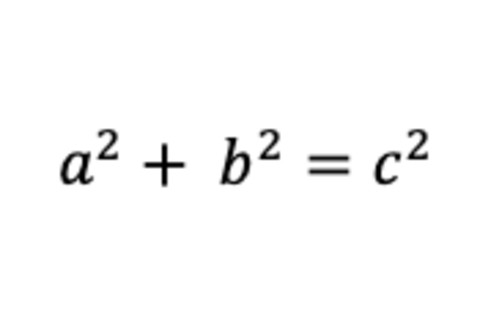
勾股定理
虽然这个方程是以公元前六世纪的希腊数学家毕达哥拉斯的名字命名的,但它的历史要悠久得多。
伯顿写道:“我们经常被告知,在数学中,所有道路都通向希腊。”希腊人自己也认为它是由埃及传下来的,现代考古学在很大程度上支持这一说法。但最早拥有这一几何瑰宝的是巴比伦人。
一份大约公元前1800年的泥板,被称为普林普顿322,上面列有勾股数——一组满足该定理的整数。例如
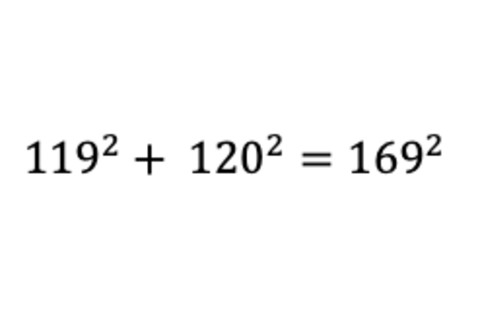
勾股数组
许多学者认为这个列表是纯粹的理论数学练习,甚至可能是用于教学学生的习题集。
然而,2021年,新南威尔士大学的数学家丹尼尔·曼斯菲尔德(Daniel Mansfield)提出了更实际的用途:他写道,这项“关于矩形的研究……似乎源于美索不达米亚测量员在测量土地时遇到的问题。”
在与普林普顿322年代相近的一首诗中,一位测量员报告说:“当人们发生争执时,我能抚平他们的心。”
3. 二次公式
二次公式,另一个代数上的重要公式,是高中生遇到的第一个真正令人望而生畏的数学结构之一。深入挖掘,你甚至可能还能回忆起老师用来让你记住它的歌谣。(提示:“Pop Goes the Weasel”旋律。)
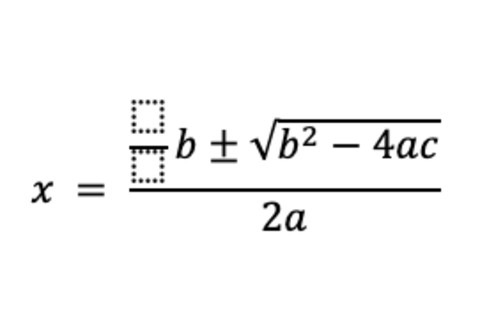
二次公式
为可能造成的二次创伤感到抱歉。更糟的是,乌塔·梅兹巴赫(Uta Merzbach)和卡尔·博耶(Carl Boyer)在《数学史》中写道,这个复杂的变量字符串“对巴比伦人来说并没有造成严重的困难。”
也许是因为他们没有以如此抽象的方式来思考它。事实上,诸如“a”、“b”和“c”之类的不定词汇尚未发明,所以他们使用了“宽度”、“长度”、“面积”和“体积”等词语。
与勾股定理一样,二次公式也有助于处理实际的行政事务。但梅兹巴赫和博耶指出,巴比伦泥板上的许多问题“似乎是智力练习,而不是关于测量或簿记的论文,它们表明了对数关系的抽象兴趣。”那时人们已经开始将数学视为一门独立的学科。
阅读更多: 你听过那个关于数学家的笑话吗……
4. 泰勒斯定理
现在该为希腊人应得的赞誉了。在无数的几何学创新中(比如欧几里得的著作),他们发现了这个非常酷的事实:如果你以圆的直径作为三角形的一边,那么另外两条边(如果它们在圆周上相交)将始终构成一个直角。证明过程太长无法在此包含,但你可以在这里看到它是如何运作的。
现在看来它可能很基础,但请记住,在公元前六世纪,泰勒斯和他的同代人正在从零开始发明演绎数学——利用逻辑推理来发现关于世界的不可辩驳的真理。他可能在一次巴比伦之行中得知了他定理的实质,但他(至少根据传统)是给出其严谨证明的人。这就是为什么它被称为“定理”,而不仅仅是“聚会技巧”。
梅兹巴赫和博耶写道:“因此,泰勒斯经常被誉为第一位真正的数学家——几何演绎组织的创始人。”
我们无法确定是谁真正创造了这个定理。泰勒斯和毕达哥拉斯都是热门人选。但既然后者因古代最著名的方程而获得荣誉,我们就让泰勒斯拥有这个。
5. 阿基米德的牛只问题
在泰勒斯之后几个世纪,希腊最杰出的数学家是阿基米德。当他不是忙于革新几何学和发明巧妙的新工具时,他有时会沉迷于伯顿称之为“披着诗歌外衣的算术问题”中。
他从《奥德赛》中的一句诗中汲取灵感:“接着你将到达特里纳西亚岛,那里养着许多牛和肥美的太阳的羊。”
阿基米德想知道到底有多少头牛。他提出的问题极其复杂,但基本上归结为两个平方数之间的差,可以用以下方式表示
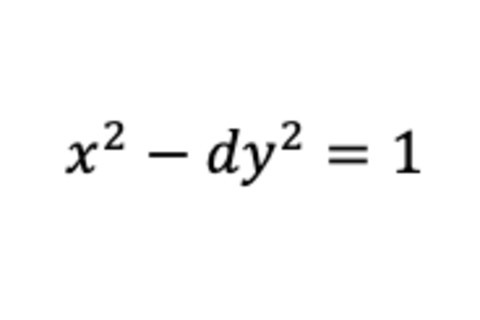
阿基米德的牛只问题
如今,这被称为佩尔方程,它被错误地以英国数学家约翰·佩尔的名字命名,尽管他迟了2000年才接触到这个领域。话虽如此,阿基米德和其他早期研究此类方程的人,都没有能力解决它们。尽管他当时不知道,但他最初的谜题要求的是求解
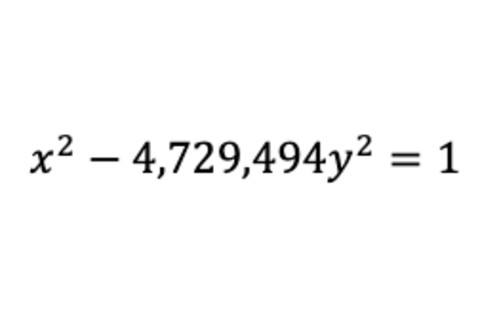
阿基米德的牛只问题,b
最终答案——在1965年借助计算机的帮助下得出——有206,545位数字。至于阿基米德和他的同伴,伯顿写道:“他们可能展示了相关的方程,然后就此事作罢。”然而,这并不能减损仅仅提出问题所需的想象力。
佩尔方程吸引了许多近代最伟大的数学家,从皮埃尔·德·费马到莱昂哈德·欧拉。在他们之前,印度数学家婆罗多笈多(Brahmagupta)和巴斯卡拉二世(Bhāskara II,分别生活在公元七世纪和十二世纪)发现了解决这些方程整数解的算法。即使在今天,人们仍在研究它们的细微之处,形成了一条一直追溯到古代的学术脉络。
文章来源
我们的Discovermagazine.com作家在文章中采用同行评审研究和高质量来源,我们的编辑会审阅科学准确性和编辑标准。请查看本文使用的以下来源
Taylor & Francis。再看公元前1850年的两个埃及金字塔体积“公式”
Britannica。勾股定理
Springer Nature。普林普顿322:矩形研究
ScienceDirect。二次方程
Math Open Reference。泰勒斯定理
Britannica。阿基米德螺旋泵
Semantic Scholar。关于Stevenhagen的猜想