在21世纪的伟大数学问题中,拼图的谜题长期以来被不公平地忽视了。现在,由于多伦多大学数据科学家 Madeleine Bonsma-Fisher 和量子物理学家 Kent Bonsma-Fisher 的工作,这种情况发生了改变,他们解决了一个困扰着全世界拼图爱好者的难题。
他们研究的核心问题是:如果你有一幅 N 块的拼图,拼好后其面积为 Aa,那么未组装的碎片会占用多大的空间?换句话说,“拼图需要多大的桌子?”而这恰好是他们关于这个主题的论文的标题。至少在某个方面,答案令人相当惊讶。
拼图碎片
Bonsma-Fishers 首先计算了拼图单块碎片的大致面积 Ap,他们指出,Ap 是拼图总面积除以碎片数量。
所以 Ap = Aa/N。如果这个形状近似为正方形,那么每条边的长度是 √Ap = √(Aa/N)
然后,他们设想在未组装的状态下,碎片是随机排列的,因此它们像圆一样分布,其直径等于其最长边。
这个直径是
d = √(2Ap) = √(2Aa/N)
圆在平面上的一种堆积方式是六边形排列,在这种排列中,每个圆都被其他6个圆环绕。研究人员指出,在一个六边形单元内有三个完整的圆,因为六个边缘圆中的每一个都包含一个圆面积的1/3,再加上中间的那个圆。这意味着当它们以这种方式堆积时,单个圆所占的面积是六边形 Ah 面积的1/3。
因此,当有 N 块碎片,每块碎片占据 Ah/3 的等效面积时,他们推导出以下公式
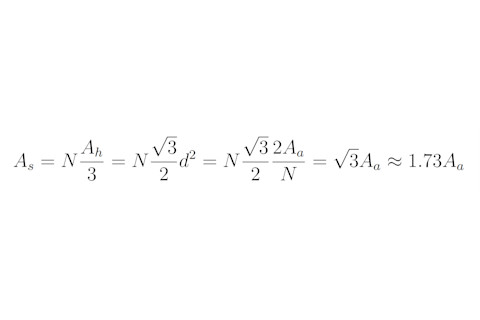
来源: arxiv.org/abs/2312.04588
换句话说,未组装拼图的面积是已组装拼图面积乘以 √3 ≈ 1.73。这令人惊讶,因为它不依赖于 N,即碎片数量。
因此,在组装之前,一块被分成20块的拼图所占用的空间,与同一块拼图被分成1000块所占用的空间是相同的。Bonsma-Fishers 用以下例子来解释这一点。
“当碎片数量少而尺寸大时,碎片之间的间隙较大(六边形晶格间距较大),但这个面积乘以碎片数量较少。反之,当碎片数量多而尺寸小时,晶格间距较小,但碎片数量较多,”他们说。“每个晶格单元都乘以 N,但每个晶格单元的面积有一个 1/N 的因子;这些因子会相互抵消,得出最终结果与 N 无关。”
他们接着通过测量各种拼图在组装和未组装状态下的尺寸来检验这一想法。“我们发现在各种拼图面积和碎片数量下,实际测量结果与我们的理论预测非常吻合,”他们说。
这是一项有趣的工作,可能会在此基础上进一步发展。想象一下三维空间中的相同问题,或许是乐高积木需要组装成模型,或者氨基酸需要组装成蛋白质。
那么问题就变成了,在组装之前,需要多少空间来存放未组装的零件?
量子问题
采用相同的方法,设想在组装之前,每个乐高积木或氨基酸都处于随机定向状态,因此它们像球体一样堆积。球体的直径等于碎片所填充立方体的对角线长度。以此类推……我们将其留给感兴趣的读者来计算答案或一系列答案。
这可能对任何在组装乐高积木之前运输乐高积木的人都有用。它甚至可能对研究蛋白质组装所需资源的生物学家有用(尽管量子搜索可能在组装过程中发挥重要作用,这可能会改变结果,因为量子物体可以共享同一空间)。
但最大的欢呼声无疑将来自拼图爱好者,他们再也不用猜测组装拼图所需的桌子大小了。
参考: 拼图需要多大的桌子?: arxiv.org/abs/2312.04588
















