今年,我们感恩一个对于我们现代理解自然力的核心概念:规范对称性。
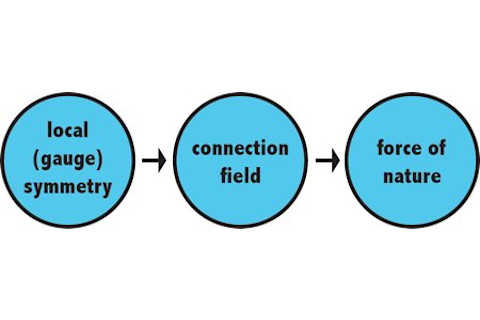
当你写一本畅销书时,你面临的最大决定之一就是选择哪些有趣但困难的概念去探讨,哪些要简单地搁置。在《宇宙尽头的粒子》一书中,我面临了关于规范对称性及其与自然力之间关系的这个问题。这个关系很容易概括:我们现代理解的四种“自然力”都直接源于规范对称性。而希格斯场之所以有趣,是因为它在我们面前隐藏了其中的一些对称性。
所以最后,认识到这是一个微妙的话题,并且讨论可能令人不满意,我还是咬紧牙关,尽力解释为什么这种对称性直接导致了我们所认为的“力”。其中一部分涉及到解释在这个上下文中“连接”是什么意思,我不太确定以前是否有人在科普书中尝试过。而且很可能以后也不会有人再尝试了!
物理学家和数学家将“对称性”定义为“我们可以对一个系统进行的一种变换,而不会改变其本质特征”。
圆具有很多对称性,因为我们可以围绕中心任意角度旋转它,旋转后它仍然是同一个圆。我们也可以沿着中线反射它。相比之下,正方形具有一定的对称性,但较少——我们可以沿着中线反射它,或者旋转90度的整数倍角度,但如果我们旋转一个不是90度倍数的角度,我们就得不到同一个正方形了。随意的涂鸦没有任何对称性;我们对它做的任何事情都会改变它的外观。这似乎不难理解。
一个抽象的层次是从一个像圆这样的有形物理对象的对称性跳到更概念化的一些东西,比如“物理定律”。但这是一个非常值得的飞跃!我们在这里地球上体验到的物理定律,就像圆一样,在旋转下是不变的。我们可以做一个实验——比如,卡文迪许实验,用来测量两个测试物体之间的引力强度——在某个给定的实验室配置下。
然后我们可以把整个实验室旋转一个固定的角度,再做一次实验。如果你做得对,你会得到相同的结果,除去实验误差。(请注意,卡文迪许实验非常困难,所以除非你真的有能力,否则不要在家尝试。)同样适用于其他类型的实验,比如测量电子电荷。
物理定律在旋转下是不变的:你可以旋转你的实验并得到相同的结果,就像旋转圆会得到相同的几何图形一样。现在再进一步,想象你在楼下的实验室里有一个朋友,也在做同样的实验。
他们会得到和你一样的引力强度或电子电荷结果。这是由于另一个对称性——物理定律在平移(位置变化)下是不变的。当然,旋转不变性仍然成立;如果有人疯狂到同时拿起两个实验室,将整个建筑物旋转一个固定的量,然后放回原处,再进行实验,我们仍然会期望得到相同的答案。
你的直觉告诉你,这不仅仅是这样,你的直觉是对的。我们不必拿起整个建筑物和里面的两个实验室;我们应该能够只旋转其中一个建筑物的装置,而不改变另一个,并且**仍然**得到相同的实验结果。
规范对称性
但请注意,这不像我们之前的例子那样,是对整个世界的单一旋转;现在我们是分别旋转两个实验,所以它们的取向相对于彼此会发生变化。这就是规范对称性:当一个对称变换可以在空间的不同点独立进行时。
规范对称性有时被称为*局域*对称性,因为我们可以在每个点独立地(局域地)进行它们;它们与*全局*对称性形成对比,后者需要在整个地方以统一的方式进行。这可能会令人困惑,因为“局域”听起来比“全局”小,而实际上局域/规范对称性代表的对称性比单纯的全局对称性要大得多——多到无限,因为变换可以在每个点完全独立地发生。够了,希望这都说得通。
这里有一个微妙之处:你怎么**知道**一个实验室相对于另一个实验室是否被旋转了?你怎么能比较不同位置实验室的方向?这似乎不是一个太难的问题;你可以使用一些测量设备,或者如果它们足够近,看看对方的实验。但你在做这件事的时候,正在利用空间本身的结构,这是如此基本以至于我们通常甚至注意不到它的存在。
特别是,我们有办法通过在它们之间来回旅行或发送某种信号来比较不同地点设置的事物。当我们旅行(或信号传播)时,我们能够追踪我们离开的地方和方向。当你仔细想想,这相当惊人。
为了比较设置在不同地点的事物,我们实际上依赖的是一个延伸到这些地点之间的**场**。我们需要的场的数学名称是连接,因为它有助于连接不同点上发生的事情。
规范场
在物理学中,它被称为*规范场*,因为赫尔曼·外尔引入了一个(无用的)类比,用“规范”来测量火车轨道之间的距离。你可以将规范场想象成一条条看不见的线条,贯穿整个宇宙,当你穿越空间时,它们会记录什么是“保持平行”以及什么是“沿直线移动”。
但是,量子场论有一个古老的基本原理:一旦有了场,这个场就可以有它自己的动力学——它可以弯曲和扭曲空间,通常是对它所相互作用的其他场的响应。当你的规范场开始扭曲时,你会感受到它,感受到一种自然力。
想象你和你的朋友在做独立的实验。如果你在同一个建筑的不同房间里,你可以在一个平坦的地板上自由移动,而且你感觉不到任何力。但如果你在户外起伏的山丘上做实验,当你走过山丘时,脚下的地面会把你推来推去。
在这种情况下,地面的结构本身就定义了一个连接场,它的曲率会产生一种力。这确实是一个接地气的例子。更根本地说,时空本身上存在一个连接场,它告诉我们如何走直线(测地线)以及比较不同点的方向。而且这个连接可以是弯曲的,而这种曲率会产生一种自然力,我们称之为“引力”。我们刚刚发明了广义相对论。
广义相对论基于一套相当直接的对称性:我们已经提到的旋转和平移,再加上“提升”(boosts),它们关联了相互运动的参考系。(总的来说,是庞加莱群。)
内禀对称性
那么其他力呢——电磁力以及强核力和弱核力?恐怕没有那么具体。这些都基于“内禀”对称性——它们不是在空间内转换事物,而是将不同的场互相旋转。例如,你可能听说过夸克有三种不同的颜色:红、绿、蓝。称某个特定的夸克为什么颜色并不重要;因此,存在一种将不同颜色互相旋转的对称性。
在数学上,它具有SU(3)群的结构,与之相关的规范场产生了强相互作用。电磁学和弱相互作用遵循一个简单的模式。胶子、光子以及W/Z玻色子都源于不同类型的连接场,这些连接场关联了不同空间点的对称变换。事实上,电磁学是我们能够理解其基于规范对称性的第一种力。
广义相对论是下一个,但有趣的是,GR直接基于时空对称性而不是内禀对称性,这使得它有点像一个特例,所以联系(原谅我的双关语)没有那么明显。(尽管它就在我的GR书中。)
在20世纪50年代,杨振宁和米尔斯大胆地提出,规范理论也可能位于核力的核心,尽管在此之前也有过类似的设想。杨-米尔斯理论没有被更早尝试并且没有立即流行起来的原因是,基于规范对称性的力乍一看似乎具有一种普遍且立即可见的特征:它们的作用范围是无限远的。广义相对论和电磁学都是如此,而且连接场的数学结构似乎暗示它应该总是如此。(这是我无论如何也想不出用通俗易懂的方式来解释的论点——有人有什么想法吗?)
用粒子物理学的语言来说,通过量化规范场得到的玻色子粒子应该是无质量的,就像光子和引力子一样。但核力的作用范围显然是短程的,所以这个想法并没有立即成功。这个困境的答案是……希格斯机制!
通过引入另一个场(希格斯场),它在空间中处处都有非零值,你可以赋予规范玻色子质量,而且这种方式完全符合数学。这个想法的胜利似乎得到了希格斯玻色子发现的证实。有趣的是,事实证明,即使玻色子仍然是无质量的,杨-米尔斯理论也不一定产生长程力。
想象一下,没有希格斯场(也没有导致自发对称破缺的任何其他效应),所以弱相互作用的W和Z玻色子(或它们对称破缺前的先驱)保持完全无质量。与光子不同,这些玻色子会直接相互作用,而且在低能量下,这些相互作用会变得非常强。
足够强,以至于弱相互作用的粒子会被禁闭,而弱力将无法延伸到很远的距离。这当然是强核力所发生的情况;胶子是无质量的,但强力被禁闭,因此作用范围是短程的。也许我们很幸运,禁闭的物理学是在希格斯机制之后才被发现的,否则后者可能需要很长时间才能弄清楚。















