我学到了广义相对论(GR)课程的宇宙学部分,其中早期会遇到的一个观点是我对思考宇宙时混淆三个截然不同的概念的传统批评。粗略地说,这些是:宇宙的形状是什么?宇宙是有限的还是无限的?宇宙会永远膨胀下去还是会重新坍缩?当我们应用 GR 到宇宙学时,我们利用了基于观测的简化假设,即存在一个时间的定义,使得在固定的时间值下,宇宙在空间上是均匀的(无论观察者在哪里看起来都一样)并且是各向同性的(在一点周围的所有方向上看起来都一样)。然后,我们专门研究最符合这些假设的通用度量,并写下由此产生的爱因斯坦方程以及相应的源(常规物质、暗物质、辐射、宇宙常数等)。这些方程的解是著名的弗里德曼-罗伯逊-沃尔克时空,描述了宇宙的膨胀(或收缩)。花点时间强调我们在这里所做的很重要。GR 确实是一个描述弯曲时空的美丽几何理论。但实际上,我们是在求解微分方程,并附加(在本例中)宇宙看起来像现在的条件。微分方程描述了系统的局部行为,因此在 GR 中,它们描述了时空点邻域的局部几何。由于均匀性和各向同性是非常严格的假设,因此在任何固定时间点,空间的局部几何只有三种可能的答案——它可以是空间上正曲率(局部上像一个三维球体)、平坦(局部上像一个平坦平面的三维版本)或负空间曲率(局部上像一个三维双曲抛物面)。GR 的给定宇宙学解告诉我们在时空点周围的其中一个答案,而均匀性则告诉我们在每个时空点周围的答案都相同。这就是当我们说 GR 告诉我们关于宇宙的几何——宇宙的形状——正如 NASA 下面的图所示。
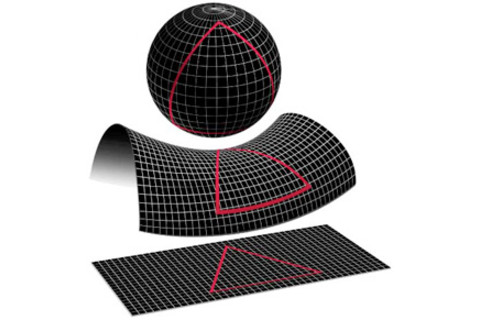
这引发了一个与上述问题截然不同的问题,而这两个问题经常被混淆。如果我们的解告诉我们,宇宙在每个时空点周围局部上是一个三维球体(或平坦空间,或双曲抛物面),那么这是否意味着它就是一个三维球体,或者一个无限的平坦三维空间,或者一个无限的双曲抛物面?这实际上是一个关于拓扑的问题——它是如何连接起来的——这也能回答宇宙是有限的还是无限的问题。为了说明这一点,假设我们已经求解了 GR 的宇宙学方程,并发现无论在哪个时空点,宇宙在局部上都是一个平坦的三维空间。顺便说一句,观测实际上表明我们的宇宙就是这样的。那么,凭你的直觉,你可以想到许多具有完全相同属性的不同空间。一个例子当然是,宇宙确实是一个平坦的、无限的三维空间。另一个例子是,宇宙是一个三环面,在这个空间中,如果你固定时间并沿着 x、y 或 z 轴从任何一点画一条线,你会遍历一个圆并回到起点。这是一个有限体积的空间,其连接方式非常特殊,但处处都是平坦的,就像无限的例子一样。在二维空间中,人们可能会将其可视化为

当然,我也可以只让一两个方向变成圆(使其在某些方向上仍然是无限的),或者将空间变成一个有多个孔的有限空间,或者其他任何可能性。这就是拓扑学的魅力,但它并不是求解 GR 方程所能告诉我们的。相反,它是我们解的额外输入。然而,这是我们可以通过测量宇宙微波背景辐射来精确检验的东西,我可能会在后续帖子中讨论。与拓扑问题完全无关,给定宇宙学解的几何形状会引发另一个经常与几何和拓扑问题混淆的问题。假设宇宙只包含常规物质源(例如,常规物质、暗物质和辐射),并且假设你知道(你可能会质疑这是否真的可能)它将永远只包含这些。那么,方程很容易预测,在正空间曲率的情况下,膨胀的宇宙最终将达到最大尺寸并在大挤压中重新坍缩,而平坦或负曲率的宇宙将永远膨胀。这些是宇宙命运的预测,并且经常导致以下联系
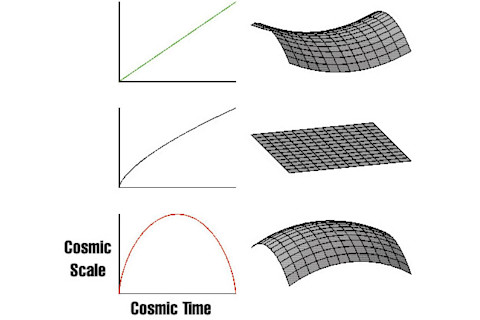
然而,正如我所明确指出的,将几何与命运联系起来存在一些假设,尽管这些假设曾经可能看起来是合理的,但我们今天知道,宇宙的加速膨胀似乎指向某种形式的暗能量(例如宇宙常数)的存在,它以一种与常规质能源截然不同的方式运行。事实上,我们知道对于像这样的源,一旦加速开始,即使是正曲率的宇宙,也很容易永远膨胀。确实,在宇宙常数的情况下,这正是发生的。因此,宇宙可能是正曲率、负曲率或平坦的,而我们对 GR 的解告诉我们这一点。它们可能是有限的或无限的,并且以有趣的方式连接起来,但 GR 并不能告诉我们为什么会这样。而宇宙可能会永远膨胀或重新坍缩,但这取决于宇宙能量预算的详细属性,而不仅仅是几何形状。宇宙时空是我们所知的 GR 最简单的解之一,即使是它们也存在各种潜在的复杂性,超出了最显而易见的选择。很奇妙,不是吗?















