去年四月,在华盛顿特区举行的美国物理学会会议上,来自三个独立实验室的代表公布了对重力强度的新高精度测量结果。令在场听众惊讶的是,这三个测量结果之间存在相当大的差异,更糟的是,它们都没有与物理学家十多年来一直接受的正确数值相符。没有人能提供哪怕一点点线索来解释这些差异。
为了说明这种困境的严重性,想象一下一个被警察追捕的重犯。他们知道他藏在一条十个街区、每个街区有十栋房子的街道上的某个地方。根据之前的信息,警方已将他们的监视重点集中在第二个街区中间的一栋特定房屋上,这时突然出现了三名新的、 presumably 可信的证人。一名证人将罪犯安置在第一个街区的第一栋房子里,第二个证人指出第一个街区末尾附近的一处住所,而第三个证人则指着镇上街道另一端的一栋房子,距离监视点超过八个街区。
测量G的实验对每一个微小的引力影响都极其敏感,从飞过屋顶的麻雀到对跖地的地震。
警察该怎么办?是选择多数意见,把行动转移到第一个街区?还是取平均值,在第三个街区附近等待?是试着挑选最可靠的证人,集中精力搜查一栋房子?还是扩大搜索范围,覆盖整个十个街区?抑或是原地不动,因为新的报告相互矛盾而对其不予理会?试图理解新测量的物理学家正面临着同样令人不满的选择。
测量的目的很容易理解。根据艾萨克·牛顿的说法,宇宙中任何两个物质物体都以与物体质量成正比并随距离减小的力相互吸引。为了量化这种现象,物理学家将G定义为两个相距一米的一公斤质量物体相互施加的引力大小。严格来说,G是一个没有直观意义的奇特量,因此物理学家们随意地用更熟悉的术语将其称为力。在这种情况下,G的值为15.0013万亿分之一磅。(G不应与g混淆,g是地球表面附近的重力加速度,也不应与g力混淆,g力是加速度对物体的影响。)
测量引力强度的概念简单性与实际操作的困难性形成鲜明对比。G的难以捉摸性有两个根本原因。首先,引力弱得可怜。如果这两个物质块的距离缩短十倍,大约四英寸,那么引力虽然会增加到100 G,但仍然不会超过大约十亿分之一磅——这相当于一个普通大肠杆菌的重量。
另一个更微妙的问题是,引力与所有其他自然力不同,它无法被屏蔽。例如,使分子不分解的电和磁力可以被中和。正电荷抵消负电荷,南极抵消北极。屏蔽使得绝缘导电体成为可能,即使它们带有220伏致命电压,也可以安全处理,出于同样的原因,依靠电磁辐射的收音机在公路隧道中会信号减弱。而引力却没有这样的屏蔽,因此测量G的实验对每一个微小的引力影响都极其敏感,从飞过实验室屋顶的麻雀到对跖地的地震。
牛顿在提出万有引力定律并用它来解释包括行星轨道、海洋潮汐和地球两极扁平化在内的大量现象时,并不需要知道G的值。同样,NASA的工程师们在精确绘制空间探测器路径时,也无需知道G的值。引力理论的大多数应用仅依赖于相对值,例如月球加速度与苹果加速度之比,这些值可以比G的绝对值更精确地确定。
事实上,G的第一次精确测量直到1797年才进行,距离万有引力定律的发现已经过去了一个多世纪,它源于英国贵族亨利·卡文迪什进行的一项经典实验。卡文迪什是个怪人。虽然据说他是“所有有学问的人中最富有的人,也很可能是所有富人中最有学问的人”,但他生活节俭,只将财富花在书籍和科学设备上。他病态地沉默寡言,病态地隐居,是一个如此坚定的厌恶女性者,以至于他只通过书面便条与他的女管家交流。
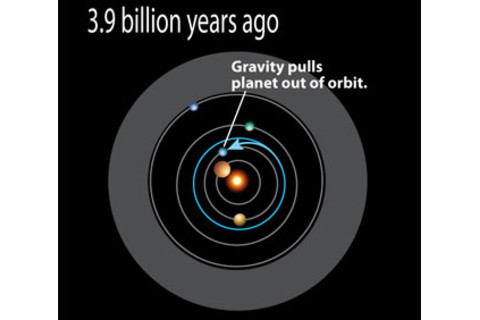
温弗里德·迈克利斯在德国不伦瑞克的小组通过两个静电发生器产生电场,将横梁的一端固定住,而另一端(未显示)则受到微小的引力牵引。横梁漂浮在水银池中。
尽管行为怪异,卡文迪什却是他那一代人中最具独创性和生产力的科学家之一。他用来测量G的巧妙装置,称为扭秤,是由牧师兼业余博物学家约翰·米歇尔建造的,并由法国电力先驱查尔斯·库仑同时发明,但在卡文迪什的巧手下,它彻底改变了精密测量科学。此后数百次对G的测定几乎都使用了扭秤。此外,它还被用于无数其他应用,例如地震测量和电气校准——凡是需要精确控制微小力的地方。
扭秤的构思基础是这样的观察:一根从天花板上悬挂下来的细长金属丝,不需要很大的力就能使其产生扭曲。(被吊死的人即使在微风中也会扭动。)如果一根水平横杆像移动杆一样悬挂在金属丝的下端,它就可以作为指示金属丝扭曲角度的指针。一旦这样的扭秤经过校准,它就成为一个测量施加到横杆一端的微小力的装置:一个微小的水平推力会导致相当大的扭曲角度。
卡文迪什将一个小铅球附在横杆的一端,将一个巨大的重物固定在球稍前方,然后观察金属丝因球被重物吸引而扭曲。(实际上,为了平衡他的装置,他在横杆的两端都放置了相同的球,呈哑铃状,并通过对称地将两个大重物尽可能靠近球而又不接触来使吸引力加倍。) 通过测量这个装置中金属丝产生的微小扭曲,卡文迪什读取了导致扭曲的实际力。由此,以及装置的测量尺寸,他能够通过简单的比例推导出G的值。结果与现代值相近,但这真是个巨大的“相近”范围。卡文迪什估计他的精度约为7%,这意味着将逃犯定位在100个街区范围内的某个地方。
现代测量的精度几乎提高了千倍,可以将罪犯锁定在一栋特定的房屋内(尽管新结果之间的分歧削弱了这一成就的光芒)。但按照当今严苛的标准,G值的不确定性仍然是天文数字。从历史上看,G是第一个物理学普适常数,但具有讽刺意味的是,它也是迄今为止最不为人所知的。现代物理学建立在光速(c)、电子电荷(e)和作用量子(h)等数字之上,这些数字决定了原子的大小。其中一些常数已测量到亿分之一的精度,另一些则测量到百万分之一的精度。与所有这些常数相比,我们对G的无知程度之粗糙令人震惊。
常数c、e和h在一个紧密的互联网络中相互纠缠,跨越了微观世界,这意味着所有原子和核性质的测量最终都必须用这些以及少数其他数字来表示。这种纠缠需要一个复杂的交叉检验和相互约束系统,有助于以令人印象深刻的精度确定基本常数。不幸的是,G不参与这些关系中的任何一个,因为引力在原子中不起作用。原子组成部分之间的引力比竞争的电场力和核力弱30或40个数量级,因此完全无关紧要。最终,G赤裸而孤傲,是基本常数中古老而不可接近的王者。
那为什么不干脆置之不理呢?为什么科学家们要将他们的精力投入到更好地确定G,而不是追求更有利可图的目标呢?目前,了解其大小并没有实际价值。天文学、地质学和太空探索都不会从新的测量中受益,因此这些都不是新实验的动机。相反,科学家们想要测量G是出于原则问题——仅仅因为它在那里。科学就是这样进步的。在19世纪后期,天文学家们努力从水星轨道中找出一个微小的异常——一个永远不会影响日历或日食预测的异常。他们测量它只是因为它在那里,丝毫没有意识到它很快就会成为关于时空革命性新概念——广义相对论——的唯一实验锚点。
同理,G的值可能突然跃居焦点。如今,物理学家们正在讨论一种万有理论,这是一个雄心勃勃的计划,旨在将所有力与粒子的描述统一到一个无缝的宏大框架中。如果他们找到了它,它将产生c、e、h和G之间的联系,这些联系将作为检验该理论的依据。在这样的检验中,古老的G有可能成为薄弱环节,除非我们更好地了解它。正是对这种可能性——而不是为了制造出某种市场产品——的担忧,激励着G的探索者们。
其中两项测量实际上是对卡文迪什扭秤实验的改进。新西兰下哈特测量标准实验室的马克·菲茨杰拉德和蒂姆·阿姆斯特朗通过精密的静电斥力抵消了装置中的引力吸引,然后他们又精确地测量了静电斥力。这样一来,横梁甚至不需要移动,从而将振荡和距离测量的不确定性降至最低。他们的结果是最近三次测量中最低的,它代表了街道上的第一栋房子。
远端的那栋房子象征着温弗里德·迈克利斯及其团队在德国不伦瑞克物理技术研究所进行的扭秤实验。他们的装置比新西兰的装置更进一步,以补偿外部影响。不仅测试球的引力吸引力被电抵消,而且地球的垂直拉力也被通过让球体浮在液态汞上来抵消。尽管不伦瑞克的物理学家无法解释他们的结果与其他结果之间巨大的差异,但他们对他们工作的完整性充满信心并坚决捍卫它。
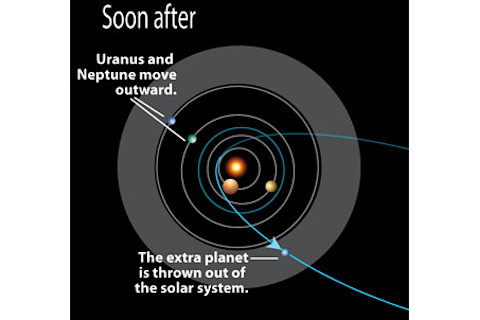

德国伍珀塔尔的欣里希·迈耶研究小组通过测量两个半吨重物(黄色)的引力将两个摆锤拉开时它们之间的距离来确定G。
第三个实验与众不同:德国伍珀塔尔大学的欣里希·迈耶团队决定另辟蹊径。他们没有使用扭秤,而是采用了一种新颖的装置来产生和测量微小的力。如果一个摆锤垂直悬挂,需要水平力才能使摆锤摆动起来。但使其产生最初的微小侧向推动所需的力极小。(因此,即使轻微的微风也会使被吊死的人摆动,甚至扭动。)这种推动力与摆锤的水平位移以一种简单的方式相关,这再次允许将小距离的精确测量转化为力的精确确定。事实证明,小距离确实可以高精度测量。
在迈耶的实验室里,两个长摆锤并排悬挂在天花板上,相距9英寸。它们的摆锤被塑造成光滑的金属镜面,彼此相对。无线电信号在镜面之间来回反弹,提供了它们之间距离的可靠测量。然后,将两个半吨重的物体推到装置外部,每个物体都靠近一面镜子。每个物体对近镜子的吸引力都比远镜子大一些,因此摆锤之间的距离会发生变化,而这种变化反过来又转化为G的测定。
伍珀塔尔方法的主要优点仅仅是它新颖,因此可以独立检验扭摆技术的准确性。此外,由于大型外部重物可以远离镜子,该实验验证了牛顿定律对距离的依赖性。这种灵活性使迈耶对他的方法的准确性更有信心。
但他并不快乐。没有一位精密测量科学家(他们喜欢这样称呼自己)会完全快乐。总会有令人困扰的问题:“我遗漏了什么干扰效应?我必须对我的数据应用什么微妙的校正因子?我如何才能提高我的精度?”当没有理论指导时,这些问题就变得更加困扰。当天文学家通过测量天空中微小的引力现象来验证爱因斯坦的广义相对论时,他们有一个目标可以追求,一个大多数物理学家都期望得到证实的数字。如果他们测量的结果不同,他们就会努力寻找、修补和调整,直到达到爱因斯坦的值,或者筋疲力尽地放弃。不幸的G值探索者们缺乏这样一个目标。他们没有理论预测应该期望什么;他们只能依靠以前测量结果的历史记录,而这些记录可能可靠也可能不可靠。他们集体遭受着一种轻微的失范状态,一种缺乏可遵循的法律和规则的感觉,一种无根的感觉。
伍珀塔尔团队对外部扰动的担忧远远超出了他们的预期。其中最令人不安的是整个设备的振动,导致两面镜子之间距离出现虚假的微观变化。数据中在中午达到峰值,凌晨3点降至最低的“噪音”很容易被忽略:那是伍珀塔尔的交通,通过夜间工作很容易消除。在考虑了当地交通后仍然存在的一种奇怪的12小时振荡周期被归因于北海150英里外的潮汐引起的微小地球运动。但一连串与交通或潮汐无关的扰动却是一个更难解决的问题。直到物理学家们解决了地震学的复杂性,这门学科与他们的训练相去甚远,他们才能够理清地震对其极其敏感的机器的影响。最终,他们不得不丢弃一组数据,因为他们发现它被半个地球之外的日本发生的轻微地震破坏了。
迄今为止,计量学家最困难的任务是决定何时停止。例如,迈耶的研究小组在发现他们错误地解释了悬挂钨丝(每根直径为0.2毫米)的引力后,已经发表了一项初步结果。这一改变使得他们测得的G值偏离了常规范围,进入了街上的第一个街区,但当然必须报告。如果他们延迟足够长的时间,他们还能想到多少这样的改进呢?他们的值最终会落在哪里?他们的实验何时结束?
为了在某种程度上解释可能遗漏的其他修正,物理学家通常会引用测量结果的数值,并附上可能的误差估计——一个值范围而不是单个数字。在逃犯比喻中,误差由房屋的宽度表示:罪犯就在里面某个地方,但我们不知道确切的位置。误差由两部分组成。第一部分称为统计误差,它简单地代表了当你多次重复任何测量以报告平均值时实际得到的结果的分布。那是容易的部分。
第二部分,称为系统误差,不过是对结果中其他可能变化的猜测。例如,如果你用金属尺测量身高,你可能会考虑到金属受热膨胀。你不知道尺子应该在什么温度下读取,但你知道在炎热天气下它不会改变超过百分之一英寸。所以你把它添加到你的系统误差列表中。计量学家使用系统误差来防范未知效应,但作用不大。
伍珀塔尔项目的发起人赫尔穆特·皮尔指出,系统误差由于其本质,通常被低估了。“如果我知道我的系统误差是什么,”他咯咯笑着说,“我就会消除它。”他轻松的态度呼应了早期一位计量学家的态度。在他的著名报告的末尾,亨利·卡文迪什谈到对G的另一个估计,该估计与他的估计相差22%,远超出他估计的正负7%的统计误差范围:“[它]与前一次测定结果的差异比我预期的要大。但在我更仔细地检查前一次测定受我无法测量的规律性影响程度之前,我暂不考虑哪种测定结果最值得信赖。”由于他尚未得出自己的系统误差估计,他采用了计量学家惯常的乐观态度,没有报告任何误差。
几乎所有关于G值测定的论文都以同样的方式结束——呼吁进行更多工作,无论是现有工作的改进,还是根本性的新方法。在世界各地的许多实验室,包括美国,对G值的新研究正在进行中。此外,还有计划在太空测量引力强度,远离交通、潮汐和地震,那里似乎可以达到前所未有的精度水平。
与此同时,最近的三次测量使G的研究陷入混乱。但这正是它应有的样子。“我们永远不会理解任何事情,直到我们发现一些矛盾,”量子力学之父尼尔斯·玻尔宣称。换句话说,科学在异常、不一致、争议和怀疑中茁壮成长。确定性扼杀了它。
















