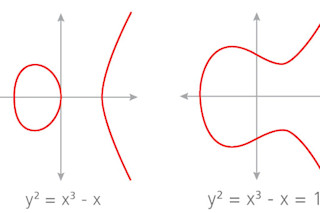
在美国高中,学生们会遇到一种连接几何和代数的虫洞:像圆和椭圆这样的几何对象与像 y^2 = x^3 –x + 1 这样的代数方程相关联。学生可以将方程的所有解可视化为圆上的点——也就是说,曲线上的每个点代表一个解。
广告
稍微增加方程的复杂性,你就会得到旋转的环和线,称为椭圆曲线。这些曲线已被证明在创建密码代码方面很有用——并且它们以其复杂性和美感让数学家们着迷。
然而,每个更复杂的曲线方程都有许多解,而且找到它们可能非常困难。数学家们为此想出了一个技巧:如果他们知道方程的某个数量的解,他们就可以利用方程和曲线之间的这个虫洞来发现方程的其余解。关键是知道需要多少解才能解锁其余的解。
十年前,一位数学家发现了一条椭圆曲线,在完全了解其完整的解集之前,需要惊人的 28 个解,这比任何人预期的都要多。这重新燃起了人们对这个主题的兴趣——有些曲线是否需要 50 个、500 个或 50 亿个解?是否存在任何限制?
事实证明,2006 年的 28 解怪物是一个罕见的例子。一篇新发表的模型在二月份发现,基于对椭圆曲线行为的统计模拟,21 个解几乎总是足够的。是的,少数特殊的方程需要 28 个或更多解,但数量不多。
到目前为止,研究人员只提出了一个概率论证,而不是一个明确的证明。但已经,这个论证及其新颖的方法导致了该领域新的想法的蓬勃发展。