虽然数学和艺术可能看起来截然相反,但对于一些艺术家来说,数学实际上为艺术家提供了丰富的灵感来源。反之,通过艺术探索这些想法也可以为相关的数学提供新的见解。这种融合可以创造出像您在这里将要看到的那些深刻而有意义的作品,这些是我们从最近的联合数学会议的竞赛展览中精选出来的,这些会议汇集了数千名具有数学头脑的人。
双曲灯罩
钩针编织,24" x 24"
Gabriela Meyer 的《双曲灯罩》是解决一个 2000 年古老数学难题的实体体现。
古希腊数学家欧几里得基于一些极其简单、看似无可争议的假设(例如“等于同一事物的两件事物也彼此相等”)推导出了令人惊讶的真理,这些真理似乎普遍适用于现实世界。但几个世纪以来,他几何学中的一个公理——一个比其他公理复杂得多的公理——一直困扰着数学家。要理解它,想象一条直线以及不在直线上的任意一点。能否通过该点画一条与已知直线平行的直线?公理说是,但只能存在一条这样的直线。
但数学家们总是想知道:能否证明这一点,而不是假设它?1826 年,俄国数学家尼古拉·罗巴切夫斯基用一个简单的答案震惊了世界:不能。他创建了一种新的几何形式,这种几何形式与欧几里得几何学相同,只是除了那个公理。在罗巴切夫斯基的几何学中,可以通过一个特定点画多条与另一条直线平行的直线。
罗巴切夫斯基的工作似乎是具有巨大理论重要性的数学奇闻——但完全不适用于现实世界。然而,在 20 世纪初,物理学家赫尔曼·闵可夫斯基意识到,像罗巴切夫斯基的非欧几里得几何学可能更适合描述我们的物理世界,尽管它们极难可视化。
现在轮到像 Meyer 这样的钩针编织者了,她是威斯康星大学麦迪逊分校的数学家。钩针编织,正如 Meyer 的灯罩所示,是帮助人们可视化罗巴切夫斯基几何学的完美工具。想象一下钩织一个通常是平坦的方块,只不过在新的一行中,针数增加了,比如说 10%。然后针数会呈指数级增长。如果第一行有 10 针,那么只经过 25 行,每行将有超过 100 针——而经过 50 行,您将有超过 1000 针!由于有这么多额外的针数,织物无法平整,因此会起皱和起波浪。
Meyer 开始钩织一个普通的螺旋。然后在边缘,她添加了比平坦空间所能容纳的更多的针数,形成了褶皱、飘逸的边缘,这些边缘可以捕捉光线或让光线穿过。
“针数增长如此之快,以至于您最终不得不停下来,”她说。“它根本无法装进欧几里得空间。”所以这个罗巴切夫斯基空间的模型可能不完美——但它很美。
关键
数字,18" x 36"
大多数艺术家使用画笔、钢笔或铅笔来涂抹颜色,但 **Etienne Saint-Amant** 使用数学公式。这些抽象的数学关系如何产生艺术作品?因为这些函数有两个特性:它们可以在二维平面上定义和表达,这自然对应于画布;Saint-Amant 可以将颜色与函数通常产生的数字相关联。这样,每个函数都转化为一幅图像。通过调整函数并重叠它们的输出,Saint-Amant 在他的艺术作品中创造了深度和情感抽象。
为了创作这幅图像《关键》中的天空和云彩,Saint-Amant 使用了一个描述灰尘颗粒在空气中随机弹跳和抖动的函数,这种现象称为布朗运动。另一个著名的函数产生了倒映的湖泊,而另一个函数(由 Saint-Amant 自己创建)产生了前景。
分形圆柱 1
数字,11.5" x 22"
高中数学老师 **Daniel Gries** 不看电视,而是通过在电脑上玩耍来放松,他编写程序来创作艺术。这件作品始于他试图让电脑不完美地画一个圆,好像是由一只摇摇晃晃的人手画的一样。一种源自分形的技术为他提供了所需的工具,在不同的尺度上产生类似抖动效果,就像结合了手指的轻微颤抖和手腕的较大抖动一样。这使他能够制作出一堆可爱的小点——假装是人手画的圆的边缘。接下来,他开始在纸上拖动他的圆,同时允许它们根据他的分形方法变形。他用不同的颜色描绘圆上的每个点,创造出这种有机、围巾状的图像。
意外的外星天使
数字,24" x 24"
**Francesco De Comité** 的《意外的外星天使》的根源可以追溯到 2300 年前的古希腊几何学家阿波罗尼奥斯·佩尔加,他的数学著作启发了阿波罗尼安垫圈的想法。
要制作一个阿波罗尼安垫圈,首先画三个相互接触的圆(数学家称之为“相切”),它们正好可以装在一个大圆内。然后,在三个圆相遇的地方,挤进第四个圆,它刚好接触其他三个圆。重复这个过程,一次又一次,永不停止——您最终会得到一种数学垫圈。它具有一个惊人的特性,那就是您放大其中一个部分看,它看起来与整体完全相同,用数学术语来说,这就是分形。
但这引出了一个棘手的数学问题:如何确定一个完美地挤进三个相切圆的第四个圆?阿波罗尼奥斯声称他知道如何做——但他提供证明的书籍已随着时间流逝而失传。文艺复兴时期的学者们听说了阿波罗尼奥斯关于如何构造第四个圆的定理的陈述,并相互挑战,试图重现他失传的证明。笛卡尔在 1643 年发现了计算新圆半径的方法,但他无法找到将其放置在正确位置的方法。直到 20 世纪 90 年代,AT&T 实验室的 Allan Wilks 和 Colin Mallows 才最终找到了这个谜题的最后一块,而且他们不得不使用计算机来完成。
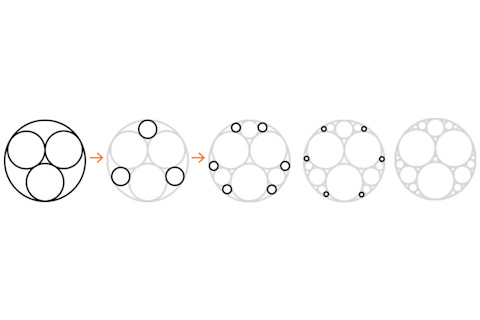
将这个过程无限地继续下去,您将得到一个阿波罗尼安垫圈。| Alison Mackey/Discover
De Comité 正在研究一个用于高效创建阿波罗尼安垫圈的计算机程序;他开始尝试各种变体,并被某些结果的美丽所打动。这张图片是他一项实验的结果。

Mojgan Lisar 和 Reza Sarhangi
蓝太阳
数字,手绘,16" x 16"
**Mojgan Lisar** 是一位艺术家,擅长塔兹伊布(tahzib),这是波斯传统上用于装饰中世纪圣书边页和扉页的风格。**Reza Sarhangi** 是马里兰州陶森大学的数学家,专门研究数学艺术,特别是波斯镶嵌。 《蓝太阳》结合了这两种波斯艺术形式。
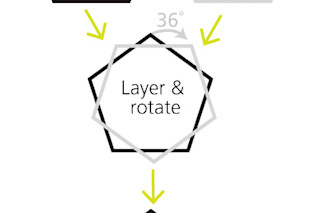
这件作品的核心构造是十角星,一种 10 角的星星,波斯艺术家因其几何特性而将其融入艺术创作中数个世纪。要创建一个十角星,取一个五边形,在上面放置第二个五边形,并旋转 36 度。五边形的星形外边缘形成一个十角星。
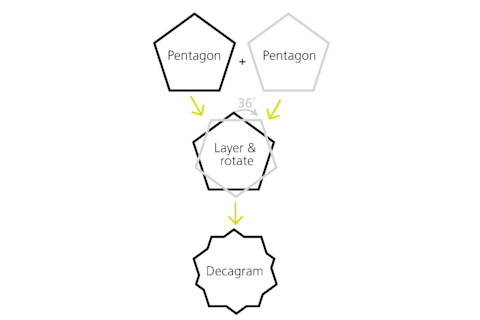
Alison Mackey/Discover
《蓝太阳》由四个同心十角星构成。Sarhangi 为十角星之间最内层和最外层的区域创建了一个波斯镶嵌图案,仅使用可以用直尺和圆规创建的形状。Lisar 为中间两个区域创建了塔兹伊布图案,带有传统的茎、叶和花卉图像。两位艺术家都采用了 10 重旋转对称性——如果您想象一根时钟指针从顶部开始,扫过十分之一的圆周,它扫过的 36 度扇形将与剩余的九个扇形中的每一个都相同。每个扇形也有其自身的反射对称性:画一条从图形中心出发将扇形分成两半的线,并沿着该线折叠。叠在一起的边将是相同的。
Sarhangi 说,波斯瓷砖艺术家是数学家,即使他们没有证明任何定理。“设计师或工匠的主要关注点是呈现视觉和谐与平衡,”他说,“不仅在细节深处,而且在整体上。尽管如此,创建此类设计所采取的步骤包括只有数学家才能获得和理解的技术。一个了解这些详细技术的人就是数学家,无论是否是艺术家。”
超棒
木雕,12" x 12" x 12"
**George Hart** 的雕塑《超棒》的奇妙之处在于它不会散架。
雕塑由两个较小的结构组成:第一个结构包含六个相互交织的平面五边形,每个五边形独立存在,不受其他五边形支撑。第二个结构包含五个互锁的四面体(三角形底的金字塔),它们也彼此独立存在。单独来看,每个结构都会坍塌,但两者相互支撑,稳定了它们空灵的漂浮状态。
“它之所以有效,是因为漂浮的四面体想要分成五块,而漂浮的五边形想要分成六块,”Hart 说。“它们在如何分开这一点上无法达成一致,所以它们最终会保持在一起。”
两个较小结构中的每一个都有 30 个侧面:六个五边形,每个有五条边;五个四面体,每个有六条边。每个五边形的边与一个四面体的边连接——这使得雕塑具有坚固性。Hart 为五边形选择了急剧波浪形的边缘,并允许他的四面体的边缘偏离直线,以波浪形先向上然后向下起伏。因此,雕塑由 30 块激光切割的木块组成,每块都包含一个五边形边缘和一个四面体边缘。
Hart 的雕塑是基于菱形三角十二面体的几何结构构建的,菱形三角十二面体最广为人知(如果为人所知的话)是《龙与地下城》中的 30 面骰子。(“三角十二面体”是个拗口的词,但它只是意味着“具有直边和平面多边形的 30 面实体”。“菱形”意味着它的所有面都是菱形——平行四边形,边长相等。)
“我认为自己是一名应用数学家,将数学应用于雕塑,”Hart 说。“三维工作能让你获得触觉理解,一种不同的认识事物的方式。就像在任何其他数学分支中一样,你会注意到似乎行得通的东西,然后你提出猜想,这会引导你证明或证伪它们。这会引出数学问题。”
[本文最初以《数学的视野》的形式印刷出版]