发现“母矿”般的数学恒等式

去年夏天，埃默里大学的 Ken Ono 与合作者 Michael Griffin 和 Ole Warnaar 一起发现了四个无限的恒等式系列——涉及变量（如 x 或 y）的数学公式，无论这些变量的值如何都成立。（例如，(a * b)x = ax * bx..）这些新恒等式是伟大的数学家 Leonard Rogers 和 Srinivasa Ramanujan 在 20 世纪初发现的两个特定恒等式的推广。 这一发现是数学领域的一个里程碑。

发现杂志：是什么促使您对 Rogers-Ramanujan 恒等式产生兴趣？

Ono：我最初是从一个著名的故事中了解到它们的。 1913 年，伟大的英国数学家 G.H. Hardy 收到了一封来自印度一位默默无闻、没有受过教育的职员的信：Srinivasa Ramanujan。信中附有九页数学公式。

其中许多公式是众所周知的，有些是错误的，但也有一些是珍品，尤其是两个。 Hardy 说它们一定是正确的，因为没有人会有想象力来发明它们。

Ramanujan 的这些特殊恒等式是什么？

它们是美丽的“连分数”的稍微复杂一点的版本

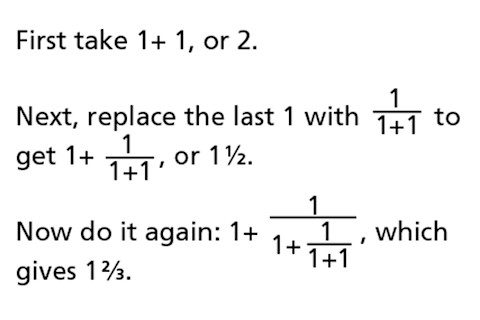
如果你永远这样做，你就会得到黄金比例，其定义是

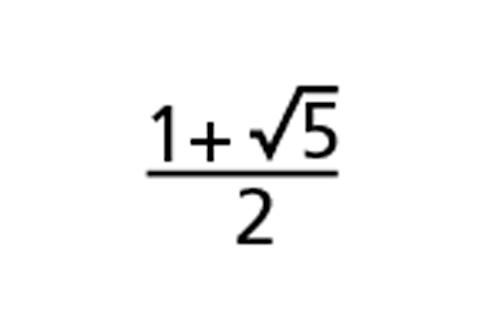
Ramanujan 以这种方式评估了另外两个连分数。 很大程度上是因为这些，专业人士 Hardy 和业余天才 Ramanujan 最终合作发明了他们那个时代一些最重要的数学。

Ramanujan 是如何提出那些吸引 Hardy 的恒等式的？

Ramanujan 有一个秘密装置：他发现了另外两个恒等式，后来被称为 Rogers-Ramanujan 恒等式。 他将特定的数字代入这两个恒等式中。

您对 Rogers-Ramanujan 恒等式发现了什么？

Griffin、Warnaar 和我发现了一个框架，它显示了它们为何正确以及它们的结构运作方式。 它们原来是两个金色的金块，表明了那里存在一整座恒等式的母矿。 我们表明，它们可以轻松地产生数学家称之为“代数”的数字，这些数字很少见，是美丽的数字，类似于黄金比例。

为什么这很重要？

Rogers-Ramanujan 恒等式与许多深奥的数学相关。 因此，这个更大的框架将开启新的数学领域。

[这篇文章最初以“一个美丽的发现”的标题发表。]