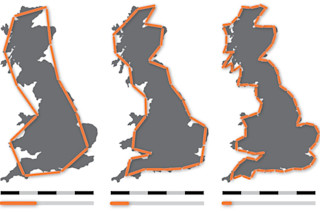
一个国家的边界有多长?这正是数学家刘易斯·弗莱·理查森在 75 多年前问自己的一个看似简单的问题。
让他困惑的是,测量尺的长度很重要。以英国为例:用 100 英里的尺子测量,你会得到一个海岸线总长度的答案。但如果将尺子缩短到一英里,它就能进入大尺子错过的海湾,答案将大得多。一英寸的尺子会给出更大的结果。
事实上,理查森意识到,答案完全取决于测量尺的长度。尺子越短,测量结果越长。推而论之,结论令人震惊:英国的海岸线是无限的。
他不知道的是,理查森刚刚偶然发现了一种此前未被认识的几何物体,这种物体注定要彻底改变传统数学。他发现了一个分形。
分形构造

雪花并非只存在于科赫的数学想象中,它们在现实生活中也形成分形。冰在空气中的尘埃颗粒周围结晶,水分子的形状导致了六边形对称。在形成的每一个瞬间,精确的大气条件决定了雪花是否会在每个点形成分支。Alison Mackey/Discover
分形就像一个无限大的俄罗斯套娃:当你放大其中一个时,你会得到一个或多或少与你开始时看到的相似的较小版本。海岸线就是一个分形,因为在任何尺度下,你都会发现海湾和峡湾——嗯,至少在达到原子级别之前是这样。
然而,在纯粹的数学领域,没有这样的实际限制。例如,考虑一下(下图中的红色)“科赫雪花”,以瑞典数学家海尔格·冯·科赫的名字命名。从一个等边三角形开始,然后在每条边上,去掉中间的三分之一,并用一个更小的等边三角形替换它。一次又一次地重复——永远如此。
你得到的结果与真实海岸线有相似之处——而且在构造它的过程中完成的步骤越多,周长就越长。永远重复下去,你将得到一个无限长的边界——尽管所有这些无限仍然包含一个有限的面积。这就像 13 世纪诗人鲁米的一句名言的数学版本:“你就是一滴中的整个海洋。”
其他著名的分形图形
Wolfgang Beyer via Wikimedia (4)
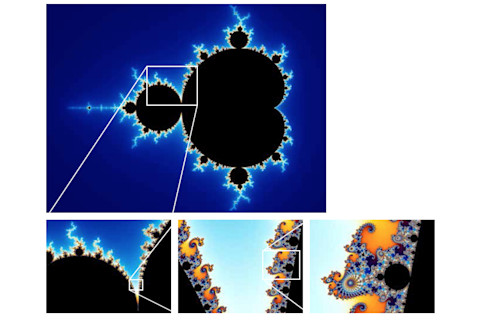
曼德勃罗集
1978 年,数学家罗伯特·W·布鲁克斯和彼得·马泰尔斯基——在解决一个截然不同的数学问题时——定义了一种基于一个相当简单的方程的新对象。但直到 1980 年 3 月 1 日,当数学家本瓦·曼德勃罗特编写程序绘制它时,这个对象的奇妙之处才显现出来。
他发现了一个前所未有的对象。在最大的尺度上,它是一种心形,带有一个圆形的尾巴。放大看,你会发现世界中有世界,形状像海马、星系漩涡和曼陀罗。但在这些奇幻形状中的每一个里面,都隐藏着最初的心形。一个简单的方程包含了整个数学宇宙。

Alison Mackey/Discover
谢尔宾斯基三角形 这是另一个你可以自己制作的。从一个等边三角形开始,将其分成四个大小相等的较小等边三角形,然后去掉中间的那个。用剩下的三个三角形重复这个过程——永远如此。你最终会得到一个谢尔宾斯基三角形,以波兰数学家瓦茨瓦夫·弗朗西谢克·谢尔宾斯基的名字命名。令人惊讶的是,它的面积为零。
维度之间的现实
分形常常具有存在于我们普通维度之间的罕见特性。
例如,科赫雪花由普通的一维线条组成,但随着迭代次数的增加,它会显得模糊,仿佛有了宽度。谢尔宾斯基三角形是由一个普通的二维三角形构建的,但由于所有的面积都被镂空了,它并不具备二维的厚重感。
曼德勃罗特通过分形维度的概念捕捉到了这一点——因此得名分形。本质上,它捕捉了分形的复杂性和锯齿状程度。再次考虑海岸线:当你缩小测量尺时,崎岖海岸线的视在长度会比光滑海滩的视在长度增长得快得多,因此它的分形维度也相应更高。
科赫雪花的分形维度约为 1.26,谢尔宾斯基三角形略高,为 1.58。曼德勃罗集的边界的分形维度为 2——这意味着它就像海岸线可能达到的最粗糙程度。直到 1991 年才证明了这一点。
大自然的偏爱图案

Scisettialfio/istock
曼德勃罗特在他的著作之一《自然的分形几何》中引入了这些思想。虽然大自然不会形成完美地无限重复的图案,但数学分形会这样做,她确实创造了一些令人惊叹的近似。
罗马内斯科西兰花,一种与西兰花相关的蔬菜,是一个特别引人注目且美丽的例子,其螺旋由螺旋组成,螺旋又由螺旋组成。

A.T. Willett/Alamy Stock Photo
闪电以其分支的树状结构形成分形图案,这意味着它具有分形维度——一项研究将其近似为 1.51。当人们被闪电击中时,由于电流在皮肤上流淌,损坏血管——而血管本身也形成分支的、类似分形状的图案,可能会形成闪电状的标记。
Champ008/Shutterstock
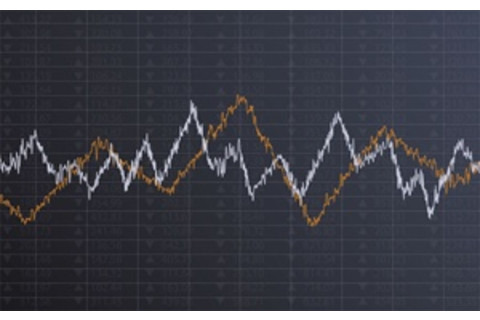
股市本身就是一个分形,有偶尔的巨大崩盘或泡沫,以及更频繁的小幅上涨和下跌。
Leonid A. Mirny and Maxim Imakaev
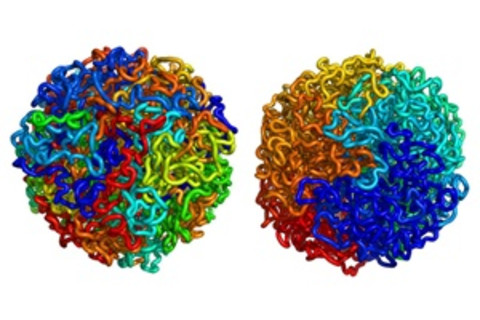
DNA 以分形图案打包进细胞。人类细胞中的 DNA 长达 6.5 英尺——比普通人还长。但它必须折叠起来才能装进一个微小的细胞核,而且细胞必须能够展开它可能需要的任何部分。分形图案做到了这一点。

Claudio Divizia/Shutterstock
蕨类植物是另一个分形例子。数学家迈克尔·巴恩斯利创造了一个蕨类植物形状的数学分形(右),很容易与真品混淆。
GSFC/NASA
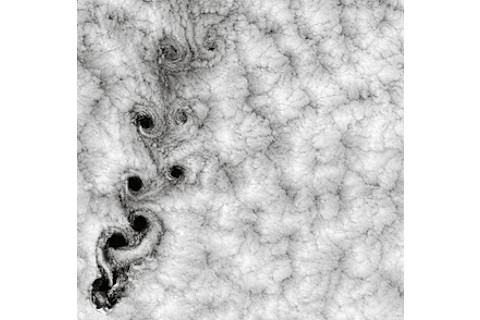
云形成分形,很可能是因为风的湍流在各种尺度上以相似的方式运行。大的温暖潮湿的空气流以热气柱上升,但其中又有较小的空气柱以自己的形状扭曲。因此,大尺度和小尺度的形成最终看起来相似。
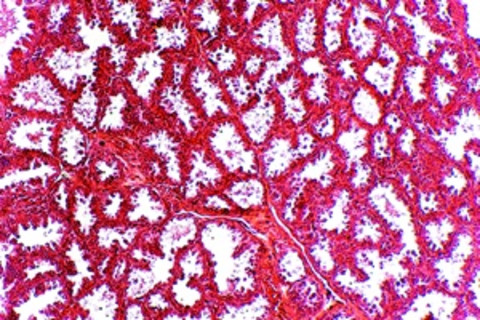
Keith Wheeler/Science Source
人乳腺组织具有分形结构,细胞排列成弯弯曲曲的形状,这些弯曲的形状中又有更小的弯曲。阿尔伯塔大学的一对研究人员分析了近 8,000 张健康和癌变组织的图像,发现癌变组织的分形维度一致较低。
分形的应用
不仅大自然喜爱分形。人类也借鉴了大自然的技巧,并在我们自己的技术中利用了分形。

Ciclotrama 20(风)绳索雕塑,Janaina Mello Landini 作,Gui Gomes 摄影
绳索:利用分形解决问题的早期例子之一涉及绳索,正如 Janaina Mello Landini 的这件名为 Ciclotrama 20 的雕塑所示。细纤维缠绕在一起形成线;线缠绕在一起形成绳;绳缠绕在一起形成缆。

动画:由于大自然使用分形,动画师可以利用这个蓝图来创造逼真的模仿。动画电影使用分形来创建波浪、雪景或风景。该技术在《星球大战:西斯复仇》中创造了逼真的熔岩模拟。分形天线:分形的各个尺度可以用于接收信号的不同波长范围,从而在小空间内实现更强大的天线。

分形压缩:由于高质量照片需要大量数据,我们通常使用“压缩”版本,它们并不完美,但也很接近。一种这样的方法会寻找图片不同尺度下的重复图案。它通常比行业标准 JPEG 文件生成更高质量的图像,但由于需要额外的处理时间,并不常见。