早在1970年,数学家约翰·康威(John Conway)创造了一个没有玩家的游戏,它完全根据初始状态演化。这个游戏设定在一个名为“细胞自动机”的计算宇宙中。这个宇宙由一个无限的网格组成,网格中的方块可以是活的或死的,并且在每个时间步,它们可以根据周围方块的状态从一种状态翻转到另一种状态。
这个细胞自动机自此被称为康威生命游戏,并以其内部涌现出的非凡复杂性而闻名。这个计算宇宙中存在着闪烁的信标、跳动着节奏的脉冲星,以及在计算天空中飞行的“滑翔机”和“宇宙飞船”。计算机科学家已经证明,这个世界可以容纳以通用图灵机和能够自我复制的复制体形式存在的计算机。
划时代的变化
事实上,没有人确切知道生命游戏的极限在哪里,计算机科学家们仍在努力解决许多未解的问题。其中一个问题与这个宇宙中图案的周期性有关。很明显,有些图案随着时间的推移不会改变,换句话说,它们的周期是一个时间步。其他的图案则每两个、三个、四个或五个时间步重复一次。
然后,在20世纪90年代,人们清楚地认识到,可以产生周期大于或等于61个时间步的图案。数学家们通过沿着形成循环的轨道发送图案信号来证明这一点。最小的可能循环需要43步才能遍历。通过增加其大小,数学家们可以使图案在任意数量的时间步内重复。
这引发了一个有趣的问题。是否有可能产生所有可能周期都重复的图案?换句话说,生命游戏是全周期性的吗?
鉴于上述证明,这归结为寻找从1到43的每个周期都重复的振荡图案的问题。前几个相对容易找到。“‘缺失中间’的周期,即15 < p < 43,特别是那些素数周期,发现起来更加困难,”纽约大学阿布扎比分校的米切尔·赖利(Mitchell Riley)及其同事表示。
但随着工作的深入,研究人员开始填补这些空白。“在新千年之初,只剩下十二个周期有待发现:19、23、27、31、34、37、38、39、41、43、51和53,”他们说。
在本世纪,计算机科学家们发现了所有这些振荡器,除了两个:19和41。
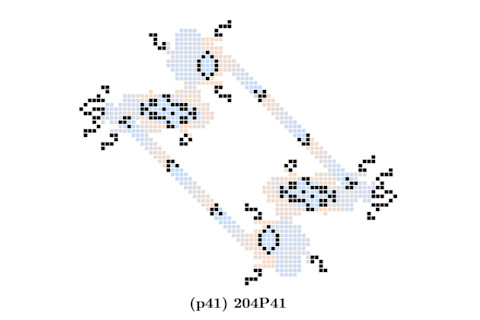
生命全周期性难题的最后一块(来源:arxiv.org/abs/2312.02799)
现在,米切尔和他的团队宣布工作已经完成。“随着最后两个周期的振荡器的发现,搜索终于结束了,”他们说。这证明了生命游戏确实是全周期性的,一劳永逸。
米切尔和他的团队的论文描述了所有这43种振荡器,以及计算机科学家和数学家为找到它们和构建功能更强大的振荡器而开发的各种技术。
他们指出,全周期性问题一直是生命游戏研究的焦点。这项工作催生了大量的技术、工具和方法,用于探索和表征这个计算宇宙。
但是现在问题解决了,接下来是什么?米切尔和他的团队指出了许多未解决的问题,这些问题可以为研究人员提供类似的焦点。他们说,宇宙飞船速度问题可能是最重要的问题。
宇宙飞船速度
宇宙飞船是一种图案,它会以相对于其原始位置的另一个位置再次出现。换句话说,它在计算天空中移动。(普通的振荡器可以被认为是静止的宇宙飞船。)
考虑到没有任何东西能在网格中以超过每单位时间一个单位单元的速度传播,作者们表示,有充分的理由认为所有可能的有理宇宙飞船速度都应该是可能的。
然而,这仍然留下了“哪些理论上可能的宇宙飞船速度可以实现”的问题,他们说。
然后是如何找到给定周期的最小振荡器的问题。他们说,许多每个周期最早被发现的振荡器已经不再是最小的了。对于许多周期来说,找到更小的振荡器的挑战仍然存在。
还有许多其他开放性问题。正如米切尔和他的团队最终总结的那样:“生命的工作永无止境!”
参考文献:康威生命游戏是全周期性的:arxiv.org/abs/2312.02799
















