1915年,两位世界顶尖的数学家大卫·希尔伯特和菲利克斯·克莱因邀请艾米·诺特前往哥廷根大学,研究一个难题。阿尔伯特·爱因斯坦当年年初提出的新引力理论——广义相对论——出现了一个问题。该理论似乎不符合一个公认的物理学原理——能量守恒定律,该定律指出能量可以转换形式但永远不会被毁灭。总能量应该保持不变。诺特,一位年轻的、没有正式学术职位的数学家,欣然接受了挑战。
她直面这个问题,证明了能量可能在“局部”——即在任意小的空间区域内——不守恒,但当空间足够大时,一切都会正常。这是她当年在德国哥廷根证明的两个定理之一。另一个定理,最终产生了更大的影响,揭示了守恒定律(如能量守恒)与自然界对称性之间密不可分的联系,这种联系已被物理学家们利用至今。如今,我们对物理世界的理解,从亚原子粒子到黑洞,都很大程度上依赖于这个现在简称为诺特定理的定理。
“我们很难夸大诺特的工作在现代物理学中的重要性,”杜伦大学物理学家露丝·格雷戈里一个世纪后说道。“她关于对称性的基本见解是我们方法、理论和直觉的基础。对称性与守恒的联系是我们描述世界的方式。”
一生勤勉
这位被两位著名数学家请来帮助解决爱因斯坦的杰作的女性是谁?表面上看,诺特(发音为NUR-tuh)似乎是一个奇怪的选择。她没有真正的数学工作,甚至很难在该领域获得教育。然而,她已经发表了一些重要的论文,希尔伯特认为她的专业知识可以帮助解决广义相对论的问题。
诺特于1882年出生于德国埃尔朗根,她希望追随她数学家父亲马克斯的脚步。但当她到了大学年龄时,德国大学不招收女性,所以诺特只能旁听课程。最终,她在期末考试中表现出色,获得了本科学位。

在她53年的人生中,她花了许多时间去对抗阻碍她追求数学的体系,诺特对代数和物理学都产生了非凡的影响。如果社会和命运对她更仁慈一些,她还能取得什么成就,我们无从得知。(来源:Emiliana and Monica Noether via Mathematical Association of America/Flickr)
Emiliana and Monica Noether via Mathematical Association of America/Flickr
1904年,她被允许在埃尔朗根大学攻读博士学位。1907年,她获得了博士学位,并在那里工作了近八年,没有报酬,也没有正式职位,依靠家人的经济支持,偶尔代替父亲代课。1915年访问哥廷根后,她留下来担任讲师,同样没有报酬。
经过多年的几乎义务劳动,诺特终于在1922年在哥廷根成为一名非终身副教授,获得了微薄的薪水。但11年后,当她和其他犹太人被纳粹德国驱逐出学术界时,她失去了工作。不久之后,她离开了德国,在爱因斯坦的帮助下,在宾夕法尼亚州的布林茅尔学院找到了一份工作。她因切除卵巢囊肿手术并发症去世,仅18个月后。
在她53年的人生中,她花了许多时间去对抗阻碍她追求数学的体系,诺特对代数(她的主要领域)和物理学都产生了非凡的影响。如果社会和命运对她更仁慈一些,她还能取得什么成就,我们无从得知。尽管如此,她的著作已经足够多,足以确保她在伟大科学家殿堂中的地位,而她同名的定理也许是她最持久的贡献。
定理的核心
诺特定理是看似无关的概念之间简单而优雅的联系,如今对物理学家来说几乎是显而易见的。但非物理学家也能抓住它的要点。
基本上,它指出自然界中每一个“连续”对称性都对应着一个守恒定律,反之亦然。让我们来分解一下这些术语。
对称性,在此语境下,是指一个对物体或系统进行的操作,该操作不会改变物体或系统的状态。将正方形旋转90度是一个“离散”对称性的例子。正方形看起来仍然一样,而旋转45度则会产生不同的形状(通常称为菱形)。然而,圆具有连续对称性,因为无论旋转多少度,甚至是一小部分度数,都不会改变其外观。这就是诺特定理适用的对称性类型。
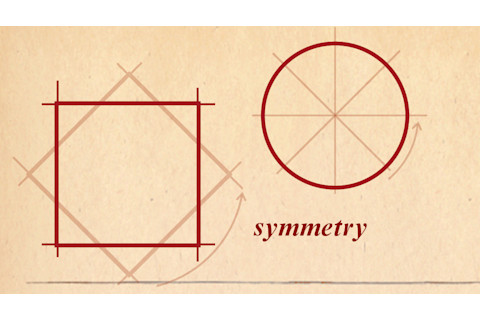
对称性(来源:Jay Smith)
杰伊·史密斯
守恒定律,是指一个物理量在时间上保持不变,因此不会随时间波动。例如,能量既不能被创造也不能被毁灭;一旦你计算出它的值,就不需要重复计算了。
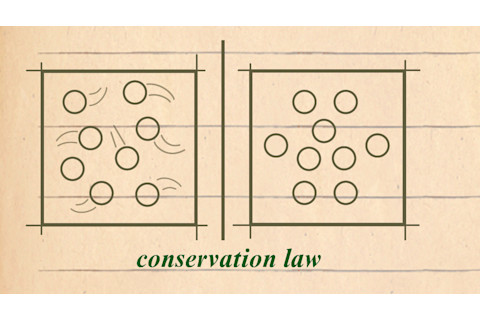
守恒定律(来源:Jay Smith)
杰伊·史密斯
诺特定理揭示了两个基本概念——对称性和守恒量——之间隐藏的关系,直到那时它们一直被分开处理。该定理提供了一个明确的数学公式,用于找到一个给定守恒定律的潜在对称性,反之亦然,找到一个给定对称性对应的守恒定律。
下面是定理应用的一个例子:想象一个曲棍球在一个完美光滑、无边无际、无摩擦的冰面上滑动。我们进一步假设没有任何外部力量作用在曲棍球上。在这些理想条件下,曲棍球将继续沿直线滑动,永不减速。它的动量,即质量和速度的乘积,将保持不变,或守恒。唯一可能导致曲棍球改变其路径,或增减速度的原因是空间本身——在这种情况下是冰面的表面——发生了变化。然而,如果冰面保持光滑,空间保持不变,那么什么都不会改变。
诺特定理表明,曲棍球的动量守恒与其“空间平移对称性”相关,换句话说,物理学不受均匀空间内直线运动(或平移)的影响。曲棍球在光滑冰面的一个区域上的运动方式与在另一个区域上相同。
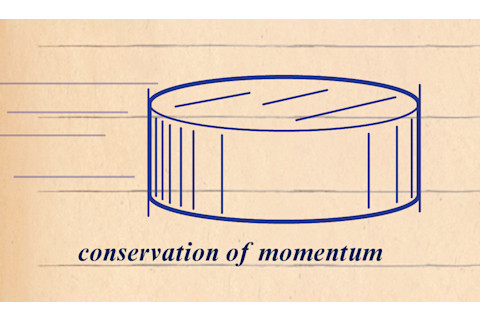
动量守恒(来源:Jay Smith)
杰伊·史密斯
类似地,诺特定理表明,旋转对称性,或称旋转不变性,导致角动量守恒,它衡量一个物体旋转的程度。换句话说,物理学没有首选方向。如果你在一张桌子上做一个实验,然后将这张桌子旋转45度,或者实际上是任意角度,实验结果都不会有差异。该定理还将“时间平移”对称性与能量守恒联系起来,因此物理学也不关心你今天、下周二还是10月的第三个星期天进行实验。

角动量守恒(来源:Jay Smith)
杰伊·史密斯
在诺特定理出现之前,物理学家们早就知道了动量守恒、角动量守恒和能量守恒。它们是经典力学的基础原则。但当时并不知道这些神圣的定律共享一个共同的起源,每个定律都与特定的对称性相关联。这一新的见解,源于诺特的工作,是一个渗透到物理学研究中的指导原则,同时也在塑造着我们对整个宇宙的看法。

能量守恒(来源:Jay Smith)
杰伊·史密斯
整合
诺特定理不仅适用于这些直观的对称性——旋转以及时间或空间的移动——也适用于更抽象的“内部”对称性,这些对称性是自然界力的基础。
例如,电荷守恒是电磁学理论的核心原则,它源于与粒子自旋细节相关的对称性。另一个例子:一种称为同位旋的对称性,它允许电子与中微子相互替换,中微子与电子相互替换,这在20世纪60年代帮助物理学家们发展了一个理论,将电磁力与弱力(解释粒子衰变和放射性过程)统一为单一的电弱力。这里的守恒量是“超荷”——一种电荷,类似于电荷,与这种电弱力相关。
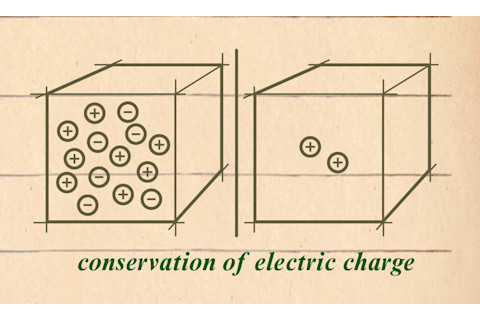
电荷守恒(来源:Jay Smith)
杰伊·史密斯
十多年后,物理学家们为强核力(将原子核中的质子和中子结合在一起)构建了一个理论。这种力的核心是所谓的色对称性。(颜色是构成质子和中子的夸克的性质,物理学家将其视为另一种电荷。)
色对称性(来源:Jay Smith)
杰伊·史密斯
在20世纪70年代,物理学家们将所有已知的粒子(包括一些尚未被证实存在的粒子,如希格斯玻色子)以及支配它们相互作用的力——电磁力、弱力和强力——置于一个称为标准模型的单一理论框架中。
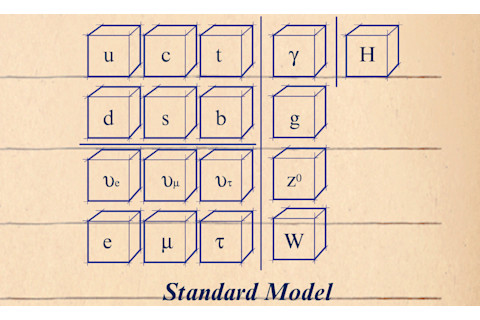
标准模型(来源:Jay Smith)
杰伊·史密斯
斯坦福大学物理学家迈克尔·佩斯金(Michael Peskin)表示,诺特定理是构建这个极其成功的模型的基础工具。“在量子力学中,你识别出两个或三个应该由对称性联系起来的粒子,然后看看推导出的守恒定律是否有效。通过这种方式,你可以了解它是否是自然界真正的对称性,标准模型就是这样建立起来的”——通过一个累积的、循序渐进的过程。研究人员现在也正试图以此为基础向前发展。
超对称遗产
寻找新粒子以及它们所源出的更深层、更广泛的对称性仍在进行中,诺特定理在这个过程中继续发挥着关键作用。目前的大部分努力都集中在寻找超对称性的迹象——这是一个假设物质粒子(费米子)与传递力的粒子(如电磁力)之间存在对称性的理论(玻色子)。如果超对称性是正确的,那么每个已知的费米子都有一个尚未被观测到的玻色子“超伴侣”,反之亦然,每个已知的玻色子都有一个尚未被观测到的费米子超伴侣。
超对称性(来源:Jay Smith)
杰伊·史密斯
加州大学圣巴巴拉分校的物理学家约瑟夫·因坎德拉(Joseph Incandela)解释说,物理学家们希望在大型粒子加速器(如大型强子对撞机)上发现的这些假想的超对称粒子,将是“所有标准模型粒子的反映,通过一个略微失真的镜子”。“镜子另一边的粒子看起来就像标准模型粒子,只是它们的自旋发生了微小的偏移。”
因坎德拉说,与这种假设的对称性相关的一个可能性是r宇称守恒,这意味着最轻的超对称粒子必须是稳定的,并且永远不会衰变。如果r宇称确实守恒,那么每个普通粒子的未被发现的超对称伴侣最终会衰变成最轻的超对称粒子,而这个粒子会永远存在。无论这个粒子是什么,它都会大量存在,因此可能是一个很好的候选者,用于解释被认为是构成宇宙物质的四分之一以上的神秘暗物质。
照亮黑洞
然而,诺特定理不仅对寻找新粒子至关重要;它还延伸到物理学的各个分支。例如,哈佛大学物理学家安德鲁·斯特罗明格(Andrew Strominger)已经确定了与软粒子相关的无限多对称性,这些粒子没有能量。这些粒子有两种:软光子(传递电磁力的粒子)和软引力子(传递引力力的粒子)。

软粒子(来源:Jay Smith)
杰伊·史密斯
斯特罗明格及其同事——剑桥大学的斯蒂芬·霍金(Stephen Hawking)和马尔科姆·佩里(Malcolm Perry)——最近发表的论文表明,落入黑洞的物质会向黑洞的边界,即事件视界,增加软粒子。这些粒子实际上充当了存储信息的记录设备,提供了关于落入黑洞的原始物质的线索。

黑洞信息悖论(来源:Jay Smith)
杰伊·史密斯
这三位物理学家提出的想法为解决物理学中一个长期存在的难题——黑洞信息悖论——提供了一种新的策略。霍金在20世纪70年代表明,每个黑洞最终都会蒸发并消失,可能会摧毁该物体曾经包含的关于它如何形成和随时间演变的所有信息。霍金的设想中信息的永久丢失让理论家们——包括霍金本人——感到不安,因为它将违反量子物理学中一条备受珍视的定律,即信息与能量一样,总是守恒的。
斯特罗明格说:“通过诺特定理,我们很快意识到存在与新对称性相对应的守恒定律,这些定律对黑洞的形成和蒸发施加了非常严格的限制。”尽管他承认这项工作仍处于早期阶段。他承认,“通过诺特定理,我们很快就意识到存在与新对称性相对应的守恒定律,这些定律对黑洞的形成和蒸发施加了非常严格的限制。”
这只是诺特定理影响巨大的另一个例子,而且例子还在不断增加。“对称性与守恒定律之间的关系是一个永无止境的故事,”斯特罗明格说。“一百年后,诺特定理仍在发现越来越多的应用。”
虽然没有人知道接下来会发生什么,但艾米·诺特定理的惊人力量和持久性是不可否认的。
史蒂夫·纳迪斯(Steve Nadis)是《Discover》和《Astronomy》的特约编辑,也是《From the Great Wall to the Great Collider》的合著者。本文最初刊登在印刷版上的标题是“根据艾米·诺特看宇宙”。

















