点击进入在试管的微观宁静中,细菌呈指数级繁殖。只要有足够的食物和空间,种群就会在几天甚至几小时内迅速翻倍。高中生物学生可能还记得这种增长的数学——类似于 P=e^rt(就像洗发水一样,教授们敦促学生记住)。电影《环太平洋》中的维度怪兽入侵地球的方式与此非常相似。在《环太平洋》中,怪兽研究员赫尔曼·戈特利布曾说:
起初,怪兽袭击间隔二十四周,然后是十二周,接着是六周,再然后是两周。最近一次在悉尼的袭击……是一周。四天后,我们可能会每八小时看到一次怪兽,直到它们每四分钟出现一次。
戈特利布关于迫在眉睫的末日的推断,有他预测下一次怪兽从“裂缝”中出现所需的数字。我们也可以这样做。不幸的是,即使让戈特利布占便宜,这些数据也毫无意义。在戈特利布的引文中,我们了解到,当怪兽首次开始出现时,每次“事件”之间的间隔是前一个时间段的一半——24周变成12周,变成6周。然后,很可能是为了戏剧效果,他跳到了每四分钟就有一只怪兽从海中出现。如果你假设事件之间的时间呈指数缩短,就像细菌的生长方式(只是反过来),你会得到类似这样的结果:
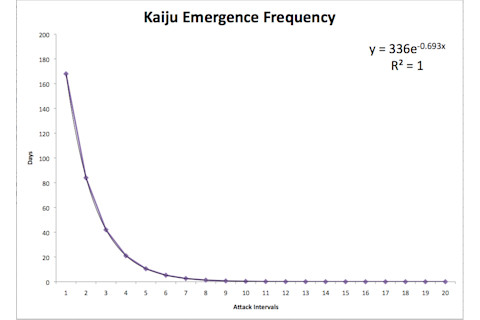
上图显示了每次出现后,袭击间隔天数缩短的速度。例如,第五只登陆的怪兽将在第四只怪兽出现后11天到达,而第四只怪兽本身是在第三只怪兽出现三周后出现的。同样,这模仿了细菌无情的生长。细菌和怪兽都遵循指数方程——在这种情况下是
y=336e^-0.693x
。这种数学隐藏着一个极其可怕的怪兽出现率。想象一个棋盘,上面放着标准的棋子。在第一个格子上放一个棋子,高半英寸。按照指数增长,在棋盘的第二个格子上放两个棋子,总高度为一英寸。在第三个格子上放四个棋子,在第四个格子上放八个,以此类推,直到达到第64个格子。仅仅按照指数增长,第64个格子上的棋子高度应该约为73万亿英里——几乎是十二光年半的高度,远远超过我们的太阳和几颗恒星。根据电影中的说法,怪兽的出现方式有点不同。与每隔一段时间就将怪兽数量翻倍不同,出现间隔时间就像反向的棋子。你开始时有很长的时间间隔,不知不觉中,每隔几纳秒就会出现一只“5级”怪兽。总之,如果戈特利布的数学是正确的,情况会很快变得末日化。但人类还有多久?考虑到怪兽袭击之间的所有时间,假设每分钟或更短时间内出现怪兽就意味着确定无疑的毁灭,那么在末日降临之前,机甲们大约还有11个月的时间。这就是数据与电影开始出现分歧的地方。根据运行此类维基百科的学术宅们所说,从第一次怪兽袭击到最后一次(当裂缝被核爆炸封印时)之间是11年。如果再次遵循数学,在出现11年后的怪兽袭击间隔时间将远远小于普朗克时间——可能是我们能测量的最小时间。而且,在这11年中,有46次被证实的怪兽袭击,而数学表明不到20次出现就意味着灭绝。至少《环太平洋》的小说和官方正典材料在忽视自身数学方面是一致的。在Nerdometrics上对怪兽袭击频率的分析中,作者列出了所有明确说明的怪兽袭击及其之间的时间。他期望找到与我计算的类似的东西——一个简单优雅的指数曲线。然而,他发现了这个:
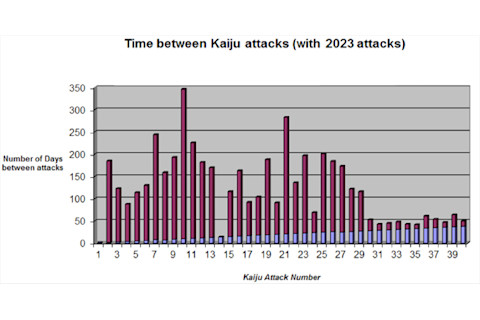
因此,单独来看这些袭击,我们看不到任何接近戈特利布在电影中如此有力地提出的数学。如果怪兽真的像细菌分裂一样出现,那将是一个巨大的问题,《环太平洋》仍然提出了一个快速取消末日的有力论据。但显然,电影在出现问题的严重程度上存在矛盾。戈特利布坚持认为数字“是我们所能接近的‘上帝之笔迹’”。赫尔曼,上帝给了你一些错误的信息——延伸阅读:《环太平洋》物理学(第一部分):火箭拳就像一架波音747打脸《环太平洋》物理学(第二部分):在海底的核爆炸气泡中图片来源:《环太平洋》海报,作者:toybot studios怪兽袭击图,来源:Nerdometrics