Amir D. Aczel (amirdaczel.com) 撰写关于数学和物理的文章,已出版 18 本书、大量报纸和杂志文章以及专业研究论文。
来自 LHC ATLAS 探测器的希格斯候选事件。图片由 CERN 提供
多年前(1972年,当我第一次遇到维尔纳·海森堡时)让我爱上理论物理的原因,是它与纯粹的数学之间令人惊叹的强大联系——远远超出了任何合理的预期。许多伟大的思想家都曾思考过抽象的数学与我们周围的物理宇宙之间这种神秘而深刻的联系,前者基于定理和证明,似乎与任何“真实”的事物都没有太大关系。除了海森堡,他巧妙地将抽象的矩阵理论应用于量子物理学,罗杰·彭罗斯在他的著作《通往现实之路》中也探讨了这两个领域——以及在某种程度上,它们与人类心灵之间的深刻关系。
1960 年,普林斯顿大学著名的量子物理学家、诺贝尔奖得主尤金·维格纳发表了一篇引人入胜的文章
试图解释这种令人惊讶的关系的神秘性质。维格纳惊叹于数学在似乎没有明显理由的情况下却能如此有效地在某些情境中发挥作用的神秘之处。然而,它确实有效。维格纳利用非常先进的数学为物理学做出了巨大贡献:他是使用数学群来模拟物理现象的先驱之一。群论是处理对称性概念的数学分支。正如维格纳帮助我们所见,对称性可以揭示物理现实最深的秘密。例如,这样的对称性使得史蒂文·温伯格能够实际预测Z玻色子的存在以及Z玻色子和两种W玻色子的实际质量,它们在物质核内起作用以产生放射性衰变。在这样做时,温伯格利用了他所谓的“希格斯机制”,他假设该机制可以打破早期宇宙的原始对称性,从而赋予这三种粒子——以及可能宇宙中所有其他物质——质量。当 7 月 4 日在 CERN 公布发现希格斯玻色子时,我们这个时代的这一极其重要的科学胜利也进一步支持了温伯格的理论。群论的“纯粹”数学能够产生如此精确的物理预测,这似乎无异于奇迹。但事实上,数学群与物理学之间的联系是由杰出的德裔犹太数学家艾米·诺特在八十年前建立的
,她 apenas 逃脱了纳粹主义,却在美国获得布林莫尔学院的教授职位后不久因腹部肿瘤去世,该学院允许她离开欧洲。诺特在数学上提出了并证明了两个关键定理,称为诺特定理。
这些强大的数学结果确立了群论的对称性与物理学中所有重要的守恒定律——例如能量守恒、动量守恒和电荷守恒——之间的关系。连续群
,挪威数学家索菲斯·李(发音为“lee”)的工作
在物理学中起着关键作用,这些通过诺特定理发挥作用。对称性在理论物理学中如何工作的技术解释超出了本文的范围,但重点在于,找到一种纯数学式的对称性可以使物理学家做很多事情:例如发现一个全新的理论!作为一个非常简短的例子:时间对称性是使物理学产生能量守恒这一关键概念的原因——能量只能改变形式(例如,根据爱因斯坦著名的公式,从质量变为纯能量),但永远不能被创造或毁灭
。* 20 世纪 60 年代,对称性风靡一时!1962 年一天,默里·盖尔曼在日内瓦 CERN 的一次国际会议上,看着黑板上写满公式的对称性,一路跑到过道,兴奋地在黑板上写下了他预测到一种新粒子存在的结论
,叫做 Omega Minus!(后来在粒子加速器工作中得到证实)
).
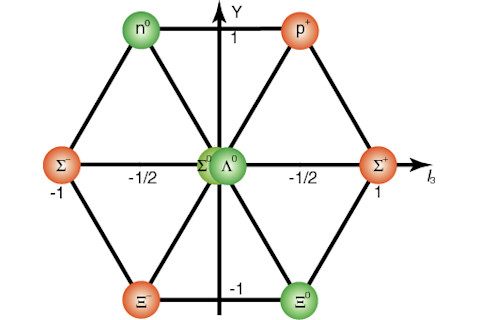
一张图说明了盖尔曼的“八重径”对称性(这早于他发现 Omega-minus 粒子及其导致的新对称性)。*** 图片由 CERN 提供
光子、Z 玻色子和两个 W 玻色子的电弱对称性被打破,因为这四种类似光子的粒子变成了 3 种有质量的粒子(因此通过希格斯机制“赋予”了它们质量),剩下一种无质量的光子(参见我之前的帖子
)。** 这种由对称性破缺产生质量的深层理论思想,从而导致了希格斯玻色子的理论诞生:即当时假设的、现在已初步证实的、与希格斯粒子相关的场的存在,它通过与电弱场的相互作用赋予了我们质量。彼得·希格斯和他的同事们(Brout、Englert、Hagen、Kibble 和 Guralnik,他们都在 1964 年提出了相同的想法)能够利用对称性的思想来预测一个粒子-波-场 的存在,该场在宇宙非常年轻时赋予了其他粒子和自身质量。因此,希格斯本身就诞生于对称性的纯数学思想,并通过连续群理论捕捉。当然,这种思想在这些论文发表之前就已经“弥漫”在空气中了,其他理论物理学家也已充分理解并从 1954 年到 1961 年发表了相关论文。但一个深刻的陷阱很快显现。一位现任麻省理工学院的物理学家 Jeffrey Goldstone(在 Steven Weinberg 和 Abdus Salam 的帮助下)证明了一个定理,该定理表明
在某些情况下,“坏”粒子——例如无质量的光子——在宇宙的原始对称性(希格斯假定在此发挥了其赋予质量的神奇作用)破缺时会以某种方式出现。这是毁灭性的消息:物理学家们不希望有这些无质量的玻色子存在,因为它们破坏了关于如何将质量赋予粒子的理论。必须对此做些什么!于是,“我们这帮 6 个人”(Higgs、Brout、Englert、Hagen、Kibble、Guralnik)出现了,技术上来说,他们所做的就是表明冒犯人的 Goldstone 定理不适用于与早期宇宙相关的特定对称性。**** 因此,随着讨厌的 Goldstone-Weinberg-Salam 定理的障碍终于被清除,最大的对称性通过电弱场与希格斯场的相互作用而急剧破缺的道路终于畅通无阻,从而赋予了 W 玻色子和 Z 玻色子质量,只留下我们孤独的光子是无质量的。因此,1964 年这一纯粹的理论进步, culminating in Weinberg's Nobel paper of 1967,使得希格斯机制得以凯旋,质量也被证明可以赋予粒子——使我们得以诞生并思考我们现在生活的宇宙的诞生。这一切都归功于对称性的数学思想以及纯数学与理论物理之间不可思议的强大联系!* 另外两个关于物理学中对称性的快速示例:爱因斯坦的广义相对论具有一个称为“广义协变性”的重要对称性——它赋予了理论力量和有效性。麦克斯韦的电磁学理论具有特定的李群结构,使得该理论即使在通过数学群的作用在抽象数学空间中“旋转”时也能保持有效。这里涉及的群是圆的所有可能旋转(任意给定角度的旋转)的群。这个李群称为 U(1)。** 这种对称性由连续群SU(2)xU(1)建模
,它是“圆旋转”群 U(1) 和特殊酉 2x2 矩阵群 SU(2) 的乘积。这个复合群被认为控制着大爆炸后不久存在的电弱对称性,并且通过其场与希格斯场的相互作用而破缺。这由Steven Weinberg、Sheldon Glashow 和 Abdus Salam解释
。
今天的完整标准模型由复合群 SU(3)xSU(2)xU(1) 表示,该模型将夸克(具有 3 种颜色电荷)添加到画面中。*** 它显示了质子、中子以及 xi、sigma 和 lambda 介子(中等大小的复合粒子)。这是李群 SU(3)(特殊酉 3x3 矩阵群)的一个表示。**** 这被称为杨-米尔斯规范对称性:一种特定的连续李群对称性。















